top of page

Derivation of various formulas for electromagnetic waves (in the case of absorbing media)

*This article is a continuation of the link below (hereafter referred to as the first part), and the equations (1) to (9) shown in this article refer to the equations in the first part.

・Equation for electromagnetic waves in absorbing media

・Application of Snell's law to absorbing media

・Application of Fresnel formula to absorbing media and energy reflectance

・Principles of ellipsometry

・Postscript

  • Equation for electromagnetic waves in absorbing media

From the previous parts (2)-①, (2)-③, and (1)-④, the equation for electromagnetic waves can be expressed as follows.

電磁波に関する様々な公式の導出（吸収体）_129.png

Therefore,

電磁波に関する様々な公式の導出（吸収体）_025.png

Here, the refractive index n is expanded to a complex number, which allows us to express the effect of absorption by the medium mathematically.

In (10)-①, the refractive index n is replaced with the complex refractive index shown below.

電磁波に関する様々な公式の導出（吸収体）_130.png

Here, κ is called the extinction coefficient.

At this time,

電磁波に関する様々な公式の導出（吸収体）_027.png

Therefore, if the light intensity is I,

吸収係数
電磁波に関する様々な公式の導出（吸収体）_026.png

Here, the absorption coefficient α is defined as follows:

吸収係数の定義式

Applying this,

電磁波に関する様々な公式の導出（吸収体）_012.png

This means that the light intensity attenuates exponentially with respect to ek・r , and 1/α represents the depth in the direction of light wave propagation from r = 0 until the light intensity becomes 1/e times. This depth is called the absorption length and is used as a guide to the depth that light can penetrate.

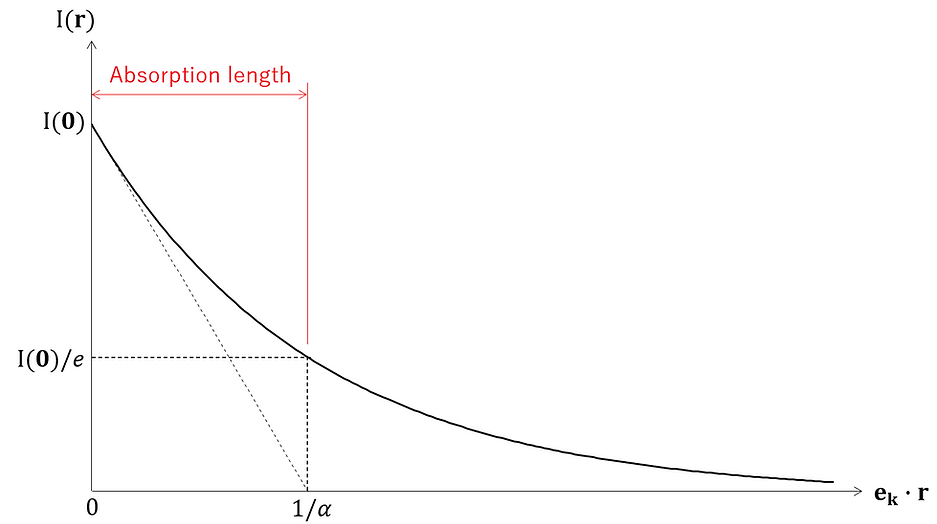
吸収長の図示

Furthermore, (10)-⑥ can be illustrated spatially as follows:

波数ベクトルと光強度の関係について図示

Here, for the sake of simplicity, ekz =0.

  • Application of Snell's law to absorbing media

The refractive index of medium 1 is n1, and the refractive index of medium 2 is n2. Also, with respect to the interface between medium 1 and medium 2, the incident angle from medium 1 is θ, and the outgoing angle to medium 2 is ξ.

電磁波に関する様々な公式の導出（吸収体）_014.png

From Snell's law derived in (4)-⑦-2 and (5)-⑦-2 in the previous chapter,

電磁波に関する様々な公式の導出（吸収体）_016.png

Here, if medium 2 is an absorbing medium, the effect of absorption by medium 2 can be expressed mathematically by replacing the refractive index n2 with the complex refractive index below, as in (10)-②.

電磁波に関する様々な公式の導出（吸収体）_131.png

In this case, since the right-hand side of (4) and (5)-⑦-2 is a real number, ξ must also be a complex number to satisfy the equation. This can be expressed as follows.

電磁波に関する様々な公式の導出（吸収体）_132.png

Here, the range of values for each parameter is determined as follows:

電磁波に関する様々な公式の導出（吸収体）_046.png

Replacing n2 and ξ in (4),(5)-⑦-2 with (11)-①-1,2 respectively and rearranging the equation gives the following:

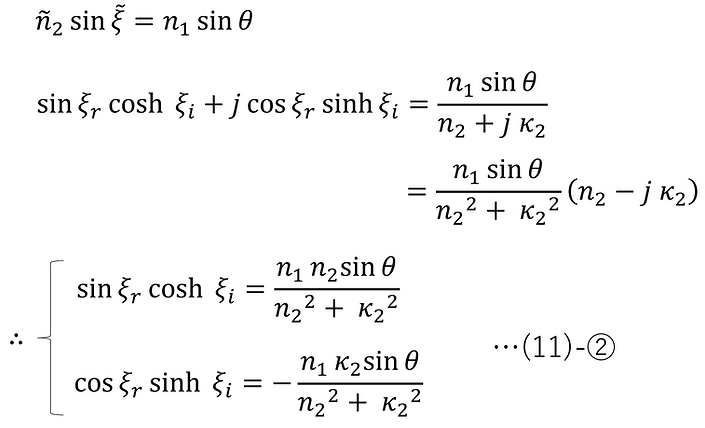
電磁波に関する様々な公式の導出（吸収体）_133.png

Here, from (11)-①-3 and (11)-②,

[ i ] When θ = 0,

ξr ＝ ξi = 0

[ ii ] When θ ≠ 0,

Since ξr ≠ 0 and ξi ≠ 0,

・Derivation of ξi :

Transforming (11)-② gives us :

電磁波に関する様々な公式の導出（吸収体）_047.png

Here, the following is set:

電磁波に関する様々な公式の導出（吸収体）_048.png

Applying this to the above equation,

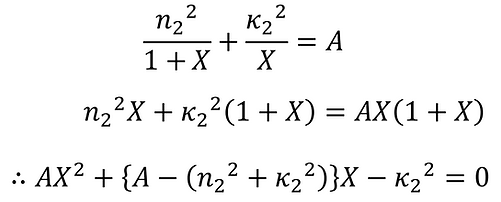
電磁波に関する様々な公式の導出（吸収体）_049.png

Since X > 0, A > 0,

電磁波に関する様々な公式の導出（吸収体）_050.png

Here, we put it as follows:

電磁波に関する様々な公式の導出（吸��収体）_051.png

Applying this to the above equation,

電磁波に関する様々な公式の導出（吸収体）_052.png

Here, from (11)-①-3 and (11)-②, the following can be said:

電磁波に関する様々な公式の導出（吸収体）_053.png

Therefore,

電磁波に関する様々な公式の導出（吸収体）_054.png

ξi can also be expressed as follows:

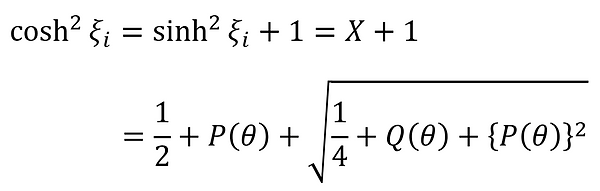
電磁波に関する様々な公式の導出（吸収体）_055.png

Here, from (11)-①-3 and (11)-②, the following can be said:

電磁波に関する様々な公式の導出（吸収体）_056.png

Therefore,

電磁波に関する様々な公式の導出（吸収体）_057.png

However, ξi < 0 (∵ (11)-③-5)

・Derivation of ξr :

Once again, transforming (11)-② gives us :

電磁波に関する様々な公式の導出（吸収体）_090.png

Here, we put it as follows:

電磁波に関する様々な公式の導出（吸収体）_059.png

Applying this together with (11)-③-1b shown previously to the above equation, we get

電磁波に関する様々な公式の導出（吸収体）_060.png

Since Y > 0, A > 0,

電磁波に関する様々な公式の導出（吸収体）_061.png

Again, applying (11)-③-2a,b,

電磁波に関する様々な公式の導出（吸収体）_062.png

Here, from (11)-①-3, the following can be said:

電磁波に関する様々な公式の導出（吸収体）_063.png

Therefore,

電磁波に関する様々な公式の導出（吸収体）_064.png

However, 0 < ξ r < π /2 (∵ (11)-①-3)

ξr can also be expressed as follows:

電磁波に関する様々な公式の導出（吸収体）_065.png

Here, from (11)-①-3, the following can be said:

電磁波に関する様々な公式の導出（吸収体）_070.png

Therefore,

電磁波に関する様々な公式の導出（吸収体）_069.png

However, 0 < ξ r < π /2 (∵ (11)-①-3)

·Summary

To summarize the above results,

電磁波に関する様々な公式の導出（吸収体）_073.png

… (11)-③-5,7, (11)-④-5,7

電磁波に関する様々な公式の導出（吸収体）_072.png

… (11)-③-2a,b

  • Application of Fresnel formula to absorbing media and energy reflectance.

[ i ] When θ=0,

At normal incidence, p-polarized light and s-polarized light are in the same state, so they are shown together.

The Fresnel formula for normal incidence (s,p polarization) derived in the previous chapter is shown below.

電磁波に関する様々な公式の導出（吸収体）_082.png

Here, by replacing the refractive index n2 with the complex numbers shown in (11)-①-1, the amplitude reflectance (s, p polarization) when incident on an absorbing medium can be expressed as follows:

電磁波に関する様々な公式の導出（吸収体）_134.png

Therefore, from (6)-④,⑦, the energy reflectance (s, p polarization) when incident on an absorbing medium is as follows:

電磁波に関する様々な公式の導出（吸収体）_136.png

[ii] When θ≠0,

​・In the case of p-polarized light

The Fresnel formula (p-polarized light) derived in the previous chapter is shown below.

電磁波に関する様々な公式の導出（吸収体）_137.png

Here, by replacing the refractive index n2 and the exit angle ξ with the complex numbers shown in (11)-①-1,2, the amplitude reflectance (p-polarized light) when incident on an absorbing medium can be expressed as follows:

電磁波に関する様々な公式の導出（吸収体）_138.png

Therefore, from (6)-④, the energy reflectance (p-polarized light) when incident on an absorbing medium is as follows:

電磁波に関する様々な公式の導出（吸収体）_139.png

However, since ξ r and ξ i are given as functions of θ in (11)-③-5,7 and (11)-④-5,7, (12)-②-2 is also a function of θ.

Here, the amplitude reflectance (p-polarized light) rp is defined as the ratio of the electric field amplitude Eip of the incident light to the electric field amplitude Erp of the reflected light, as shown below. However, since the left-hand side is expanded to complex numbers, the amplitudes of the electric fields on the right-hand side must also be expanded to complex numbers. This is called the complex amplitude.

電磁波に関する様々な公式の導出（吸収体）_175.png

​・In the case of s-polarized light

The Fresnel formula (s-polarized light) derived in the previous chapter is shown below.

電磁波に関する様々な公式の導出（吸収体）_080.png

Here, by replacing the refractive index n2 and the exit angle ξ with the complex numbers shown in (11)-①-1,2, the amplitude reflectance (s-polarized light) when incident on an absorbing medium can be expressed as follows:

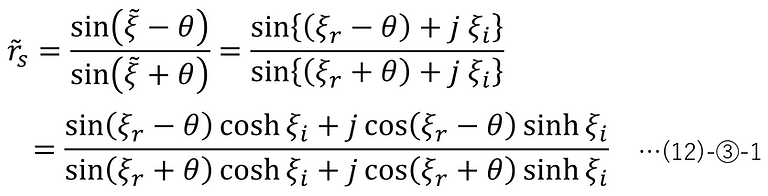
電磁波に関する様々な公式の導出（吸収体）_140.png

Therefore, from (6)-⑦, the energy reflectance (s-polarized light) when incident on an absorbing medium is as follows:

電磁波に関する様々な公式の導出（吸収体）_141.png

However, since ξ r and ξ i are given as functions of θ in (11)-③-5,7 and (11)-④-5,7, (12)-③-2 is also a function of θ.

Here, the amplitude reflectance (s-polarized light) rs is, by definition, expressed as the ratio of the electric field amplitude Eis of the incident light to the electric field amplitude Ers of the reflected light, as shown below. However, because the left-hand side is expanded to complex numbers, the amplitudes of the electric fields on the right-hand side must also be expanded to complex numbers. This is called the complex amplitude.

電磁波に関する様々な公式の導出（吸収体）_176.png

​・Case studies

If the refractive index of aluminum at a wavelength of 589.3 nm is 1.44 and the extinction coefficient is 5.23, the relationship between the incident angle θ and the energy reflectance when light is incident on aluminum from the air can be calculated using (12)-②,③-2, and the following graph is obtained.

電磁波に関する様々な公式の導出（吸収体）_089.png

It is important to note that in a non-absorbing medium, there is a Brewster angle, which is the angle at which the reflectance of p-polarized light becomes zero, but in an absorbing medium, there is no angle at which the reflectance becomes zero, so the Brewster angle cannot be defined in the sense of the angle at which the reflectance becomes zero.

  • Principles of Ellipsometry

So far, we have expanded Snell's law and Fresnel's formula to complex numbers, thereby broadening their scope of application to absorbing media. Applying this principle makes it possible to measure thin film thickness and evaluate optical constants (refractive index, extinction coefficient, etc.), composition ratio, surface roughness, crystallinity, etc. We will now derive the basic principles of ellipsometry, the analytical technology that makes this possible.

​・Derivation of the definition formula of ellipsometry

First, we examine the following range of values:

電磁波に関する様々な公式の導出（吸収体）_171.png

From (11)-②,

電磁波に関する様々な公式の導出（吸収体）_092.png

If n2 > n1 , then

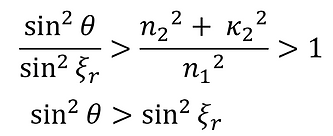
電磁波に関する様々な公式の導出（吸収体）_103.png

Therefore, from (11)-①-3,

電磁波に関する様々な公式の導出（吸収体）_104.png

Also, from (11)-①-3 and (13)-②-1,

電磁波に関する様々な公式の導出（吸収体）_172.png

Based on (13)-②-1,2,3 and ξi < 0 (∵(11)-③-5), when n2 > n1 , (12)-②-1 and (12)-③-1 can be expressed as follows using the amplitude and argument :

電磁波に関する様々な公式の導出（吸収体）_142.png
電磁波に関する様々な公式の導出（吸収体）_144.png

Here, the blue part in the formula indicates that the case distinction has been incorporated into the formula, where the value of θ+ξr is zero when it is less than π/2, and is -π when it is greater than π/2.

And, from (11)-③-5,7 and (11)-④-5,7, ξr and ξi can be expressed as functions of θ.

By applying this result, the Fresnel amplitude reflection coefficient ratio ρ defined in ellipsometry can be expressed as follows using the phase difference Δ and the amplitude ratio angle ψ (these are called ellipsometry parameters):

電磁波に関する様々な公式の導出（吸収体）_191.png

However, the domain of the phase difference Δ is set to 0 ≤ Δ ≤ 2π . If the value of (13)-④-2 is outside this range, simply add 2mπ (m is an integer) and select the value of m so that it falls within the domain.

For example, when n=1.44 and κ=5.23, ψ and Δ are calculated using θ as a variable as follows:

電磁波に関する様々な公式の導出（吸収体）_112.png
電磁波に関する様々な公式の導出（吸収体）_198.png

・Description of electric field vectors for p- and s-polarized light in absorbing media

Let us now review the electromagnetic wave equation. If the electric field vectors of the p- and s-polarized incident light are Eip and Eis respectively, the electric field amplitude vectors of the p- and s-polarized incident light are EAip and EAis respectively, and the wave vector of the incident light is ki , then from the previous chapter (2)-①, these relationships can be expressed as follows:

電磁波に関する様々な公式の導出（吸収体）_177.png

Here, the unit vector of the electric field amplitude vector of p-polarized and s-polarized incident light is defined as follows:

電磁波に関する様々な公式の導出（吸収体）_178.png

In this case, (13)-⑤-1,2 can be rewritten as follows:

電磁波に関する様々な公式の導出（吸収体）_179.png

Similarly, if the electric field vectors of the p- and s-polarized reflected light are Erp and Ers respectively, the electric field amplitude vectors of the p- and s-polarized reflected light are EArp and EArs respectively, and the wave number vector of the reflected light is kr, then from the previous chapter (2)-①, these relationships can be expressed as follows:

電磁波に関する様々な公式の導出（吸収体）_180.png

Here, the unit vector of the electric field amplitude vector of p-polarized and s-polarized reflected light is defined as follows:

電磁波に関する様々な公式の導出（吸収体）_181.png

In this case, from (12)-②-3 and (12)-③-3, (13)-⑧-1,2 can be rewritten as follows:

電磁波に関する様々な公式の導出（吸収体）_182.png

​・Description and illustration of electric field vectors of p- and s-polarized light in ellipsometry

In ellipsometry, the incident light is set as follows.

電磁波に関する様々な公式の導出（吸収体）_183.png

In this case, the following holds true from (12)-②-3, (12)-③-3, and (13)-④-1.

電磁波に関する様々な公式の導出（吸収体）_184.png

(13)-⑦-1,2 can be rewritten as follows by applying (13)-⑪.

電磁波に関する様々な公式の導出（吸収体）_185.png

This is linearly polarized light tilted at π /4 (45 degrees) with respect to the p-axis (or s-axis). This state can be achieved by using a linearly polarized laser in monochromatic ellipsometry, or by passing white light through a polarizer in spectroscopic ellipsometry.

Also, (13)-⑩-1,2 can be rewritten as follows by applying (13)-③-1,2, (13)-④-2, and (13)-⑪.

電磁波に関する様々な公式の導出（吸収体）_193.png

Therefore, when viewed on the time axis, p-polarized light leads Δ/ω ahead of s-polarized light.

Based on the above, ψ and Δ can be illustrated on the time axis as follows:

電磁波に関する様々な公式の導出（吸収体）_194.png

Here, the electric field of the incident light is shown with the absolute value normalized to 1 in addition to the condition (13)-⑪.

In this way, a phase difference Δ occurs upon reflection of linearly polarized incident light, and the reflected light generally becomes elliptically polarized light.

The polarization changes depending on the value of Δ as shown in the diagram below. When Δ=0,π, the light is linearly polarized, and otherwise it is elliptically polarized, but the direction of rotation (clockwise and counterclockwise) is reversed before and after Δ=0,π.

電磁波に関する様々な公式の導出（吸収体）_195.png

Furthermore, (13)-⑭-1a and 2a can also be expressed as follows:

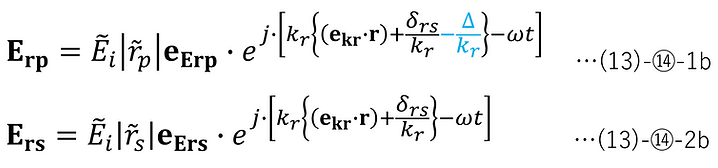
電磁波に関する様々な公式の導出（吸収体）_196.png

Therefore, when viewed on the spatial axis, p-polarized light is delayed by Δ/kr relative to s-polarized light.

Therefore, ψ and Δ can be illustrated on the spatial axis as follows:

電磁波に関する様々な公式の導出（吸収体）_197.png

Here again, the electric field of the incident light is normalized to 1 in absolute value in addition to the condition (13)-⑪.

  • ​Postscript

Conventions for the signs of phase differ between physics and optics. Here we use the conventions of physics; see below for differences between this and optics.

bottom of page