・結像関係の式の導出
物点からの光線が、焦点距離fの光学素子を介して、像点に結像する様子を図示すると、以下のようになる。
※寸法表記については、付録:1次元ベクトルと角度の方向と符号の定義について を参照
(i) f > 0, z < 0 の時、

(ii) f > 0, 0 < z < f の時、

(iii) f > 0, f < z の時、

(iv) f < 0, z < f の時

(v) f < 0, f < z < 0 の時、

(vi) f < 0, z > 0 の時、

倍率をβとすると、三角形の相似の関係より、(i)~(vi)の全て共通で以下のことが言える。

何故ならば、(i)~(vi)は全て同じモデルの一形態だからである。そのため、(i)~(vi)のうちのどれか一つのみについて考えればよい。
次に、以下について考える。

図より、以下のことが言える。

(1)-①'、(1)-②a、(1)-②bより、
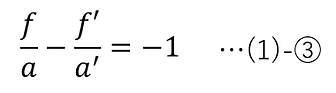
ラグランジュの不変量より、

(1)-④、(1)-②abc、(1)-①' より、

(1)-①、(1)-⑤ より、

次に、縦倍率αを以下のように定義すると、(1)-①、(1)-①’、(1)-⑥より、

これは、zが微小量のときのみに成り立つ点には注意が必要である。
※媒質が空気の場合:
n=n'=1より、以下のことが言える。

(1)-①、(1)-①'、(1)-⑧より、以下のニュートンの式(またはニュートンの関係式)を含む関係式が得られる。

次に、(1)-③に(1)-⑧を適用することで、以下のガウスの結像式が得られる。

次に、物像間距離について示す。
物像間距離を、物点を始点、像点を終点とする1次元ベクトルで定義すると、以下のように表すことができる。
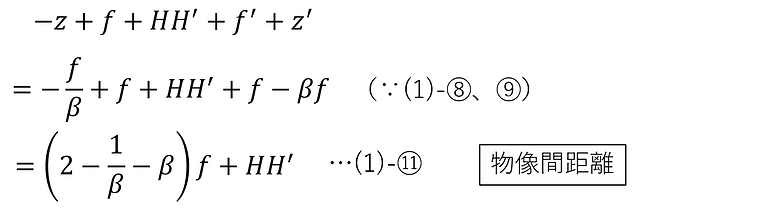
次に、縦倍率においては、(1)-⑦にn=n'=1を代入することで、以下の式が得られる。

・理想レンズによる幾何学的光線伝播の漸化式モデル
1. 漸化式のパラメータの定義
第0面(物体面)、第1面、第2面、…、第 i 面、…、第 n 面(像面)まで順に光線が通る系を考える。このとき、第 i 面のパラメータを図示すると以下のようになる。

・光学素子の前側焦点から前側主点までの距離: fi
・光学素子の後側主点から後側焦点までの距離: fi'
・光学素子の主点間距離: HH’i
・光学素子の後側主点から次の光学素子の前側主点までの距離: di
・物側空中像から光学素子の前側焦点までの距離: zi
・光学素子の後側焦点から像側空中像までの距離: z'i
・光学素子位置における光線高さ: hi
・像側の光線角度: θi
・原点位置(第0面物体面)から光学素子の前側主点までの距離:Li
但し、設定値を青字、漸化式から計算される値を黒字とした。
2. 漸化式の導出
次に、漸化式を求めるため、第i面と第i+1面について以下に図示する。
※寸法表記については、付録:1次元ベクトルと角度の方向と符号の定義について を参照

但し、ここでも設定値を青字、漸化式から計算される値を黒字とした。
図に示されている条件を式で表すと、以下のようになる。

ここで、第2式・第3式はニュートンの式を表す。
ここで、媒質を空気とし、(1)-⑧を適用する。
また、θi、θi+1を微小量とする。
このとき、(2)-①を整理すると以下の漸化式が得られる。

3. 漸化式の初項の導出
次に、漸化式の初項を得るために、第0面と第1面について図示すると、以下のようになる。
※寸法表記については、付録:1次元ベクトルと角度の方向と符号の定義について を参照

但し、ここでも、設定値を青字、漸化式から計算される値を黒字とした。
図に示されている条件を式で表すと、以下のようになる。

ここで、第2式はニュートンの式を表す。
ここで、媒質を空気とし、(1)-⑧を適用する。
また、θ0、θ1を微小量とする。
このとき、(2)-③を整理すると、以下のように漸化式の初項が得られる。

よって、各面の設定値の値を与え、(2)-②と(2)-④の計算を第0面から第n面(像面)まで順に行うことで、光線追跡をすることができる。
・光線の初期値の設定
次に、第0面の設定値 h0, θ0 の与え方について考える。
方法はいろいろ考えられるが、ここでは入射瞳位置と物体側開口数を用いて記述する方法について示す。
物体高 y0、入射瞳までの距離 zp、物体側開口数 NAo(>0)を設定することで下図に示す5本の光線(ray1, ray2, …, ray5)を与えることができる。

ここで、hpは入射瞳半径である。角度φ(>0)を微小量とすると、NAoは以下のように表すことができる。

よって、ray1, ray2, …, ray5の各光線を表す、第0面の設定値h0, θ0はそれぞれ、以下のように求められる。
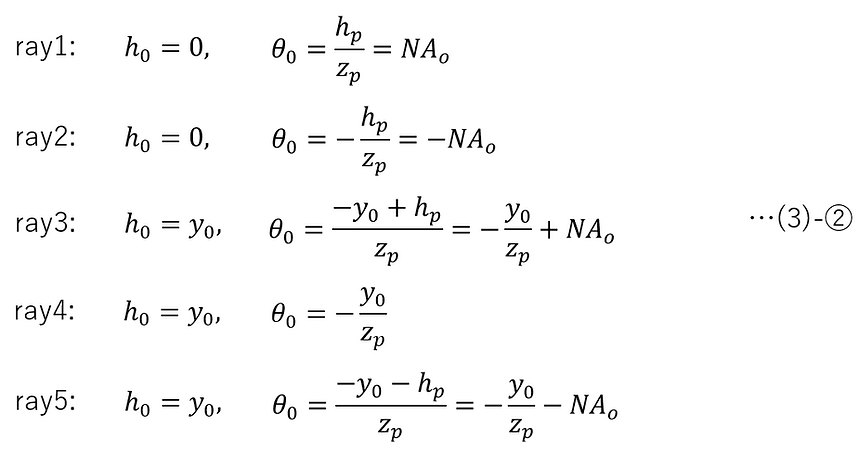
・光線の終値の計算
最後に、光学系・像面の各パラメータを自動計算で求める。
ray1(またはray2)について、第n-1面の光学素子を通った後、光線が中心軸と交わる位置を像面(第n面)になるようにdn-1を計算をする。
このとき、ray1について、第n-1面から第n面(像面)までの光線を図示すると、以下のようになる。

ray1について図に示されている条件を式で表すと、以下のようになる。

ここで、媒質を空気とし、(1)-⑧を適用すると、以下が得られる。
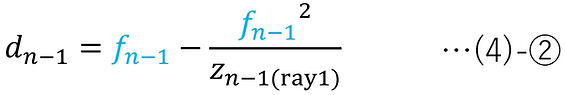
そして、像面位置におけるray3の光線高さhn(ray3)を用いて、以下を計算す�ることで、光学系全体の倍率βを求めることができる。
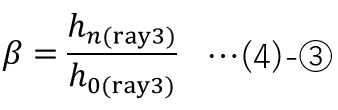
更に、像側開口数NAiは以下のように計算できる。

また、ray4については、第n-1面の光学素子を通った後、光線が中心軸と交わる位置は、射出瞳位置である。第n-1面の後側主点から射出瞳までの距離をdn-1(p)とし、また、像面から射出瞳までの距離をzp'とする。
このとき、ray4について、第n-1面から射出瞳面までの光線を図示すると、以下のようになる。
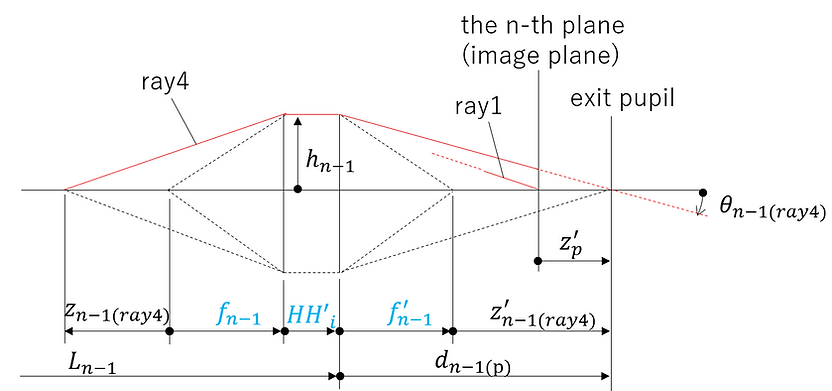
ray4について図に示されている条件を式で表すと、以下のようになる。

ここで、媒質を空気とし、(1)-⑧を適用すると、以下が得られる。

よって、射出瞳位置zp'は以下のように計算できる。

・光線追跡のフォーマット作成
ここまで示した漸化式を適用し、理想レンズを配置して光線追跡を行うフォーマットをエクセルで作成する事例について示す。
・入力部:
以下の黒い枠内に各設定値の値を入力する。第9面まであるが、全て入力する必要はなく、余った面については、焦点距離は無限大に相当する十分に大きな値、主点間距離と面間距離については値を零にしておけばよい。
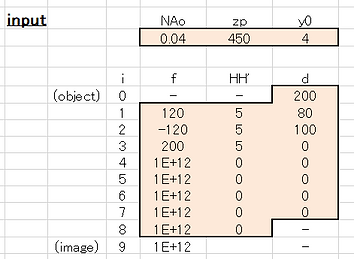
・計算部:
ray1からray5まで、それぞれ別々に光線追跡の計算を行う。赤と青の枠内は入力値を参照している。

・光線追跡用データ部:
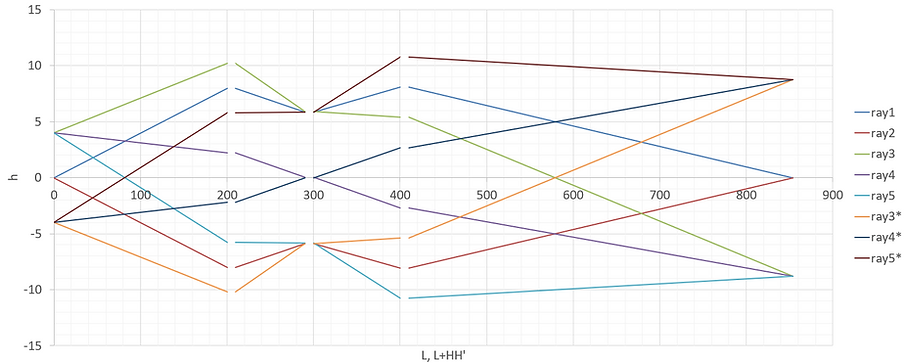
以下は、光線追跡の結果を図にするためのデータである。光軸方向の位置は、各面についてLとL+HH'で与えている。また、主点間の光線を描かないようにするため、行を空けてある。ray3,4,5においては、これらを光軸に対し反転させたray3*,4*,5*を新たに追加した。

・光線追跡結果表示部:
光線追跡の結果を図にすると以下のようになる。また、光学系・像面の各パラメータの計算結果も併せて表示させた。
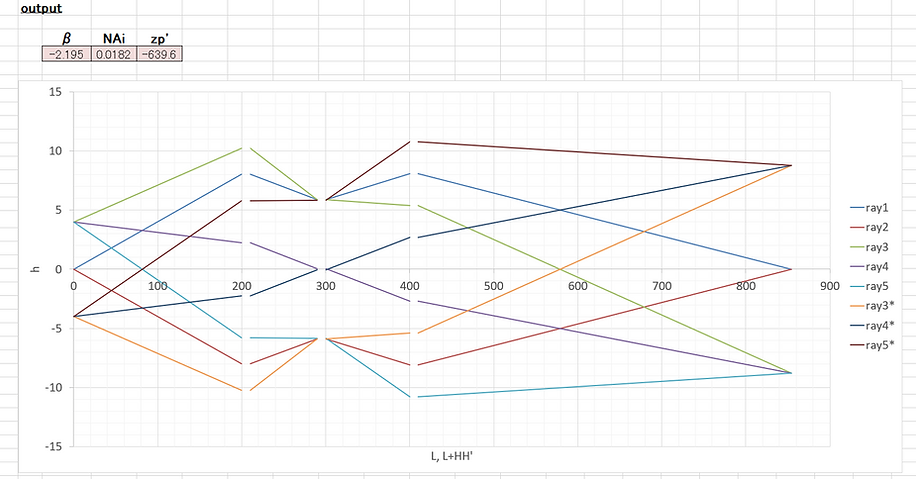
以上のようにして、エクセルを用いることで、理想レンズを配置して光線追跡を行うことができる。このフォーマットを以下に掲載する。