理想レンズ系における
ガウシアンビーム伝播の漸化式モデル
目次：
-
ガウシアンビームの形状
そもそもガウシアンビームとは何か。ガウシアンビームとは、光の進行方向に垂直などこの断面においても、強度分布が正規分布（ガウス分布）となる光波のことであり、レーザー光がこれに該当する。図で表すと以下のようになる。
図1-1
ここで、各変数は以下で定義される。
z：光の進行方向位置
w(z)：位置zにおけるビーム半径
r：中心軸からの距離
I(r,z)：位置zにおけるr方向光強度分布
I0(z)：位置zにおける中心軸における光強度
光強度分布 I(r,z) において、光強度が中心軸（r=0）における光強度 I0(z) に対し1/(e^2) 倍になるときのrの値を、位置 z におけるビーム半径 w(z) と定義する。このとき、I(r,z)は以下のように表せる。
また、各パラメータは以下で定義される。
λ：波長
L：ビームウエスト位置
wo：ビームウエスト半径
ZR：レイリー長
θ：発散角
各パラメータの色分けについては、（後に示す漸化式モデル中で）設定で与える量を青字、計算式で与える量を黒字とした。
ビーム径が最も細くなる位置をビームウエストと言い、ビームウエストにおけるビームの半径をビームウエスト半径と言う。位置 z におけるビーム半径 w(z) は、ビームウエスト位置 L とビームウエスト半径 w0 と波長 λ を用いて、以下のように表される。
z = +∞ で、(1)-②は以下に収束する。
この漸近線の傾きを、発散角 θ と定義する。
ビームウエストから、ビーム径がその√2倍まで広がる位置までの距離をレイリー長と言い、その間をレイリー領域と言う。これはレーザービームがどの程度まで広がらずに一定の径を保つことができるかを示す指標として重要である。レイリー長 ZR は以下で表される。
(1)-②に、z = L ± ZR を代入して計算すると、定義通り、w(z) = √2 w0 となることが確認できる。
-
理想レンズ系におけるガウシアンビーム伝搬
次に、光学素子を介したガウシアンビーム伝搬を考える（光学素子は収差のない理想レンズとする）。図示すると以下のようになる。
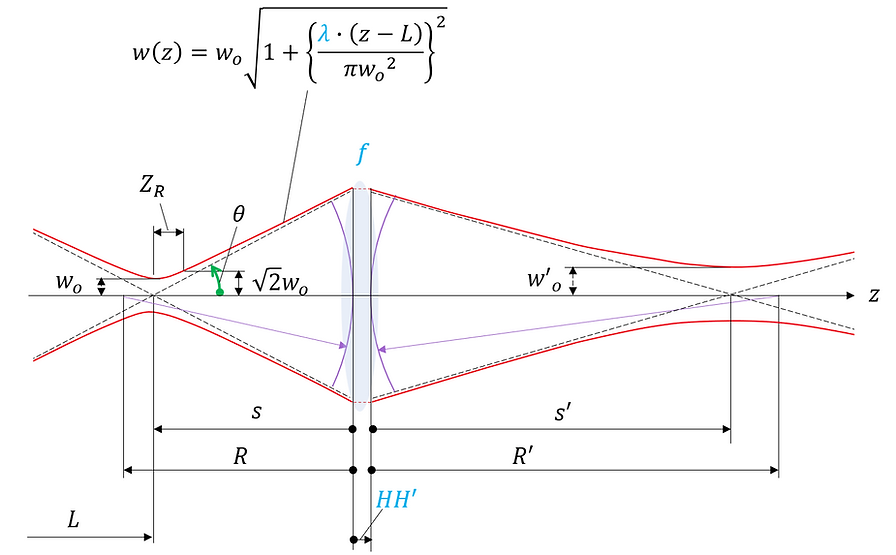
図2-1
※寸法表記については、付録：１次元ベクトルと角度の方向と符号の定義について を参照
上図の各パラメータで、図1-1で示したのと同じものについてはそれを踏襲し、それ以外の新規のものは以下のように定義する。
f : 光学素子（理想レンズ）の焦点距離
HH'：光学素子の主点間距離
R：光学素子に入射する直前の波面の曲率半径
R'：光学素子を出射した直後の波面の曲率半径
s：光学素子からビームウエスト（光学素子を通る前）までの距離
s'：光学素子からビームウエスト（光学素子を通った後）までの距離
各パラメータの色分けについては、（後に示す漸化式モデル中で）設定で与える量を青字、計算式で与える量を黒字とした。
各パラメータを求める計算式を以下に示す。
(2)-①bより、RとR'の関係はガウスの結像公式と同じ形をしていることが判る。即ち、Rの球心位置とR'の球心位置の関係は、幾何学的な光線追跡における物面と像面の関係と同じである。一方、ビームウエスト位置s, s'の関係を示す(2)-①cは、ガウスの結像公式と似ているが若干異なった形をしている。これは、幾何学的なモデルのガウスの結像公式に、光の回折の影響を考慮した補正をしたものであり、1983年にSidney Self 等によって提唱された式である[1]。
(2)-①c より、
ZR / f をパラメータとして、s / f と s' / f の関係を図示すると以下のようになる。
図2-2
ZR / f =0 は幾何光学のガウスの結像公式と同じ状態を意味する。このとき、s / f = -1 の前後においてs' / f は±∞に発散する。ここから ZR / f の値を大きくしていくと、s' / f は有限の上限・下限値を取るようになり、また、s / f = -1 のときには s’ / f = 0となる。更に ZR / f の値を大きくしていくと、s' / f の取り得る値の範囲は狭まっていく。このことは即ち、レンズを通してビームウェストを伝搬できる距離は有限であり、この距離をできるだけ遠くにするためには、（伝搬前の）レイリー長 ZR はできるだけ短く、焦点距離 f はできるだけ長くする必要があることを意味する。
-
理想レンズ系におけるガウシアンビーム伝播の漸化式モデル
次に、光学素子を順に並べてガウシアンビームを通すときのビーム伝搬の漸化式モデルを考える（光学素子は収差のない理想レンズとする）。図示すると以下のようになる。
図3-1
※寸法表記については、付録：１次元ベクトルと角度の方向と符号の定義について を参照
ここで、各パラメータの i の添え字はビーム入射位置から i 番目の光学素子に関する物理量を表す。また、各パラメータについて、設定で与える量を青字、計算式で与える量を黒字とした。
上図の各パラメータで、図1-1、図2-1で示したのと同じものについてはそれを踏襲し、それ以外 の新規のものは以下で定義する。
di：i 番目の光学素子から i+1 番目の光学素子までの距離
i 番目の光学素子に関する各パラメータを求める計算式を以下に示す。
・(1)-①②③⑤の各パラメータに添え字の i をつけると以下のようになる。
・(2)-①の各パラメータに添え字の i をつけると以下のようになる。
次に、i 番目の光学素子と i+1 番目の光学素子の間で成り立つ漸化式は以下のようになる。
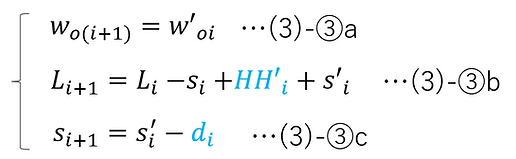
ここで、図3-1において、光学素子に入射する直前・直後のビーム径は同じ径で描かれているが、それは実際にそのようになるからである。そのことについて以下に示す。
i番目の光学素子に入射する直前・直後のビーム径をそれぞれ計算すると以下のようになる。
よって、i 番目の光学素子に入射する直前・直後のビーム径は等しいことが示された。
次に、漸化式の初項について示す。図示すると以下のようになる。
図3-2
ここでも、各パラメータについて、設定で与える量を青字、計算式で与える量を黒字とした。
上図に示すように、woi の初項 wo1 は設定値として与えられる。また、Li の初項 L1 と si の初項 s1 は、設定値 s'0, d0 を用いて以下のように表される。
-
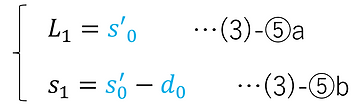
理想レンズ系における実際のガウシアンビーム伝播の漸化式モデル
(3)-①aより、woi と θi の積は i に依存しない定数となる。これを BPP（Beam Parameter Product）と定義する。
また、実際のビームのビーム半径をwoi_real 、実際のビームのビーム発散角を θi_real とすると、woi_real とθi_real の積もまた、i に依存しない定数となる。これを BPPreal と定義する。
(4)-①aと(4)-①bの比を取ることで、以下に示すビーム品質を表す量のM2（Mスクエア）が得られる。(4)-①aと(4)-①bのどちらも i に依存しないので、M2もまた i に依存しない量である。このことは、光学素子の収差の影響がなければ、任意のどれか一つの i に対してビーム半径とビーム発散角を実測すればM2の値を求められることを意味する。
M2の値は1以上であり、値が1に近い程、理想的なガウシアンビームに近いことを意味する。
ここで、実際のビームの想定について、理想的なガウシアンビームに対し正規分布（ガウス分布）を保ったままビームが広がっているものとし、M2はその度合いを表している。そのため、正規分布自体が大きく崩れているビームに対しては、十分な近似ができない点には注意が必要である。
前章の理想的なガウシアンビームと同様に、光学素子（理想レンズ）を順に並べてガウシアンビームを通すときのビーム伝播を、実際のビームについて考える。ここでは、ビームの実測は光学系に入射する前（即ち漸化式の初項）の位置で行うものとする。図示すると以下のようになる。
図4-1
※寸法表記については、付録：１次元ベクトルと角度の方向と符号の定義について を参照
ここで、各パラメータの i の添え字はビーム入射位置から i 番目の光学素子に関する物理量を表す。また、各パラメータについて、設定で与える量を青字、計算式で与える量を黒字とした。また、計算で求められる全ての量（M2以外）は、理想的なガウシアンビームとは異なる値になるので、区別のため、"real"を添え字として入れた。
上図の各パラメータの定義は、図1-1、図2-1、図3-1で示したのを踏襲する。
i 番目の光学素子に関する各パラメータを求める計算式を以下に示す。
・(3)-①の黒字の各パラメータに"real"の添え字をつけると、以下のようになる。
・(3)-②の黒字の各パラメータに"real"の添え字をつけると、以下のようになる。
同様にして、i 番目の光学素子と i+1 番目の光学素子の間で成り立つ漸化式は、(3)-③より以下のようになる。
次に、漸化式の初項 について示す。図示すると以下のようになる。
図4-2
ここでも、各パラメータについて、設定で与える量を青字、計算式で与える量を黒字とした。
漸化式の初項において何を設定値とするかについてはいくつかのケースがあるが、ここでは、woi_real の初項 wo1_real と θi_real の初項 θ1_real を設定値として与える。これらは実測によって与えられるか、または、ファイバ入力の場合はファイバのモードフィールド径が 2 x wo1_real に相当する。
このとき、M2は以下で与えられる。
Li_real の初項 L1_real と si_real の初項 s1_real は、設定値 s'0, d0 を用いて以下のように表される。
-
エクセル計算のフォーマット
ここまで説明してきた計算モデルを使って、実際にガウシアンビームの伝播をシミュレーションするエクセルフォーマットを作成しましたので、是非ご利用ください。