近軸計算に基づいた
球面レンズ系の光線伝搬
近軸領域にある光線は、光学系の光軸に対してなす角 θ が非常に小さく、かつ、その経路がすべて光軸の直近を通る。このとき、θに関して以下の近似が成り立つ。
sin θ = θ, tan θ = θ, cos θ = 1
そのため、近軸領域に限定することで光線追跡の計算は非常に簡便になり、光学系の骨格を把握する上で有益である。ここでは、その計算式の導出について示す。
・近軸計算の式の導出
物質の境界面(球面形状)を光線が透過するとき、近軸領域で��の光線を図示すると、以下のようになる。
(i) u > 0, u' > 0 のとき、

図1-1
(ii) u > 0, u' < 0 のとき、

図1-2
※寸法表記については、付録:1次元ベクトルと角度の方向と符号の定義について を参照
上図の各パラメータは以下のように定義される。
n: 境界面の入射前の材質の屈折率
n': 境界面の出射後の材�質の屈折率
r: 境界面の曲率半径
u: 境界面への入射光線が中心軸と成す角度(時計反対周りを正)
u’: 境界面からの出射光線が中心軸と成す角度(時計反対周りを正)
i: 境界面への入射光と境界面の法線とが成す角度(時計反対周りを正)
i’: 境界面からの出射光と境界面の法線とが成す角度(時計反対周りを正)
φ: 境界面への光線の入射位置における法線と中心軸とが成す角度(時計反対周りを正)
h: ��境界面における光線の中心軸に対する高さ
s: 境界面への入射光が中心軸と交わる位置までの、境界面からの距離
s’: 境界面からの出射光が中心軸と交わる位置までの、境界面からの距離
ここで、角度u, u’, φ, i, i'と高さhは十分に小さいとする。また、各パラメータの色分けについては、(後に示す漸化式モデル中で)設定で与えられる量を青字、計算式で与えられる量を黒字とした。
このとき、図に示されている条件を式で表すと、(i)と(ii)のどちらにおいても、以下のようになる。

ここで、(i)と(ii)のどちらも同じ式で表されるということは、どちらも同じモデルの一形態であることを意味し、どちらか一方で考えればよいことが言える。
(1)-①abcより、以下が導出される。

また、スネルの法則より、近軸領域においては以下のことが言える。
(1)-①’ab、(1)-②より、以下に示すアッベの不変量が導出される。

この式は以下のように変形できる。

これに(1)-①aを適用すると、以下の関係式が得られる。

・ラグランジュの不変量の導出
まず、(1)-③(アッベの不変量)に着目する。この式は、点Pから点P'に向かう光線の記述であるが、��この中には u, u', h が含まれていないことが判る。このことから、近軸領域においては、点Pを通る任意の光線は、点P'に向かう(即ち、点Pと点P'は共役の関係にある)ことが言える。このことを改めて下図に示す。
また、元の系全体を、点O(境界面の球心)に対し回転させて、点Pが点Q、点P'が点Q'に移ったとき、点Qと点Q'も共役関係にあるが、このとき、境界面は系全体を回転させる前後で全く変わっていないことから、系全体を回転させる前における点Qと点Q'もまた共役関係であることが言える。
ここで、近軸領域においては円弧PQ、円弧P'Q'はそれぞれ中心軸に対し垂直な直線と見做せるので、PQベクトル、P'Q'ベクトルは中心軸に対し垂直なベクトルである。

図2-1
上図の各パラメータについて、図1-1,図1-2で示したものについては踏襲し、新規のものは以下のように定義する。
y��:物体高
y’:像高
ω:物体高 y から、境界面と光軸の交点に向かう光線の角度
ω’:境界面と光軸の交点から、像高 y' に向かう光線の角度
このとき、図に示されている条件を式で表すと、以下のようになる。

また、スネルの法則より、近軸領域においては以下のことが言える。
(1)-①a、(2)-①ab、(2)-②より、以下の関係式が得られる。

この関係式は、ラグランジュの不変量、または、ヘルムホルツ・ラ�グランジュの不変量と呼ばれている。
・近軸計算の漸化式
第0面(物体面)、第1面、第2面、…、第 j 面、…、第 k 面(像面)まで順に光線が通る系を考える。ここで、各面は球面形状とする(平面は曲率半径無限大で与える)。このとき、第 j 面を通る前後において近軸領域での光線を図示すると、以下のようになる。
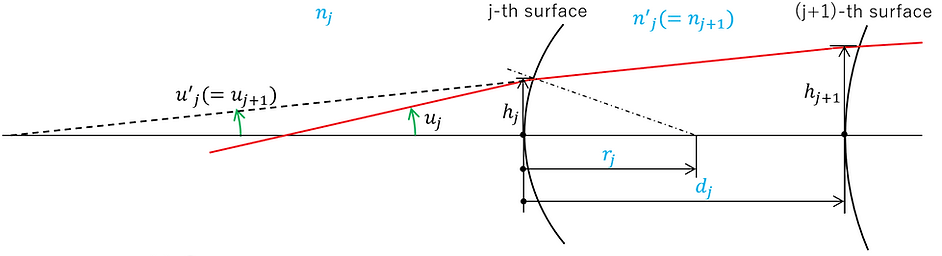
図3-1
※寸法表記については、付録:1次元ベクトルと角度の方向と符号の定義について を参照
各パラメータの j の添え字は、第 j 番目の境界面を意味する。
上図の各パラメータについて、図1-1,図1-2に示したものについては踏襲し、新規のものは以下のように定義する。
dj: 第j面から第j+1面までの距離
ここでも、角度uj, u'j, と高さhjは十分に小さいとする。また、各パラメータについて、設定で与えられる量を青字、計算式で与えられる量を黒字とした。
まず、(1)-③''より、第j面において以下のことが言える。
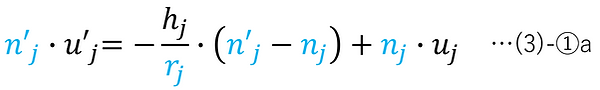
また、図より以下のことが言える。

ここで、以下のように置く。

これを(3)-①abに適用すると、以下の式が得られる。

(3)-①a'b'は以下のように行列で表すことができる。

(3)-①'abを統合すると、以下の漸化式が得られる。

次に、(2)-③(ラグランジュの不変量)より、第 j 面において以下のようになる、

ここで、n'j=nj+1, u'j=uj+1, y'j=yj+1 であるから、以下のことも言える。

(3)-③④より、以下のことが言える。

・近軸計算による光学系パラメータの導出
ここで、次の2つのケースについて、初期条件と出力値を与える。
(i) 平行光入射の場合
このとき、下図のように、漸化式の初項条件(物体面を出た先)と漸化式の終端条件(第k面を出た先)を与え、また、焦点距離 f を光学系パラメータの出力値として得る。

(1)-①aより、

よって、dkは以下の計算で求めることができる。

また、図より、焦点距離 f は以下の計算で求めることができる。

ここで、平行光入射の場合はd0はその後の計算に影響を与えない。また、近軸領域の定義としてはh0はあくまで微小量であるが、焦点距離の計算は(微小量に限らず)h0の値に依存しない。
(ii) 有限系の場合
このとき、下図に示すように、漸化式の初項条件(物体面を出た先)と漸化式の終端条件(第k面を出た先)を与え、また、倍率 β を光学系パラメータの出力値として得る。

(1)-①aより、

よって、dkは以下の計算で求めることができる。

(3)-⑤(ラグランジュの不変量)より、倍率 β は以下の計算で求められる。
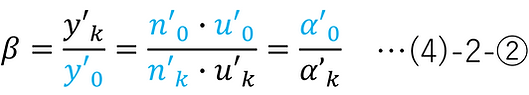
ここで、近軸領域の定義としてはu'0はあくまで微小量であるが、倍率の計算は(微小量に限らず)u'0の値に依存しない。
ここまで説明してきた内容に基づいた計算フォーマットを以下に掲載する。
・具体例:単レンズの焦点距離の計算式
ここでは、近軸計算の式から単レンズの焦点距離の計算式の導出を行う。材質の屈折率n、第1面と第2面の曲率半径がそれぞれr1とr2、中心厚をd1とし、これらを近軸計算のモデルに当てはめると、下図のようになる。
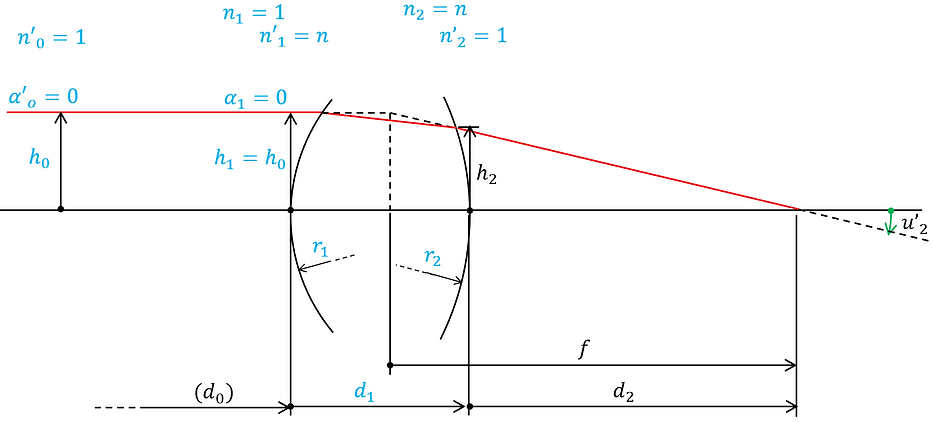
まず、(3)-①'ab、(3)-①''から以下の近軸計算式を得る。

また、(4)-1-①②より、以下が得られる。

(5)-①に図中の各パラメータ値(h1=h0, n1=n'2=1, n'1=n2=n, α1=0)を適用すると、以下が得られる。

(5)-②ab、(5)-③、図中のn'2=1より、以下が得られる。

得られた(5)-②b'は、レンズメーカーの公式と呼ばれている。