電磁波に関する様々な公式の導出
(吸収がある媒質の場合)
※本編は、以下リンク(以後、前編と呼ぶ)からの続きであり、本編中に示す式の(1)~(9)は前編の式を指すものとする。
-
吸収がある媒質における電磁波の式
前編 (2)-①, (2)-③, (1)-④より、電磁波の式は以下のように表すことができる。

よって、

ここで、屈折率nを複素数に拡張する。それにより、媒質による吸収の影響を数式で表すことができる。
(10)-① において屈折率nを以下に示す複素屈折率で置き換える。
ここで、κを消光係数(または、消衰係数)と呼ぶ。
このとき、

よって、光強度を I とすると、

ここで、吸収係数αを以下のように定義する。

このとき、

これは、光強度が ek・r に対し指数関数的に減衰することを意味し、1/αは光強度が1/e倍になるまでの r = 0 からの光波進行方向への深さを表す。この深さを吸収長と言い、光が侵入できる深さの目安として用いられる。
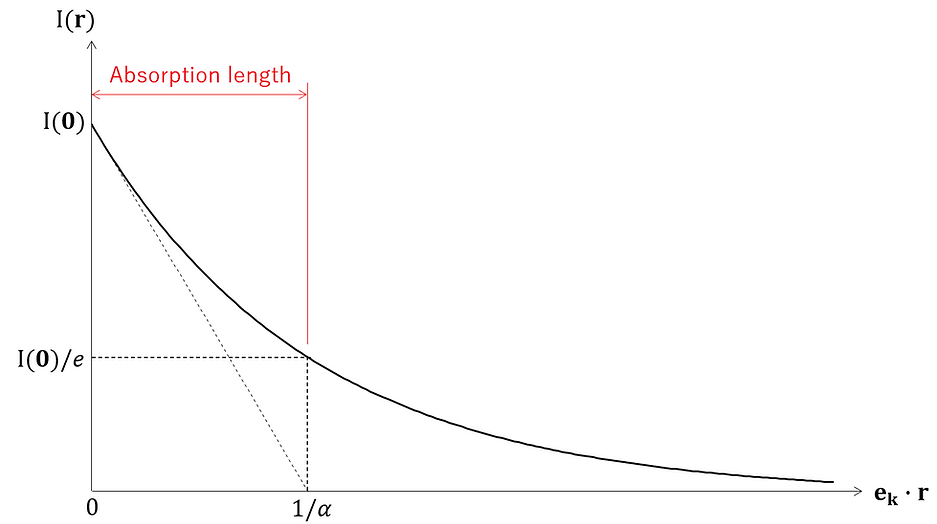
また、(10)-⑥を空間的に図示すると以下のようになる。

ここで、図の簡略化のため、ekz=0とした。
-
吸収がある媒質へのスネルの法則の適用
媒質1の屈折率をn1、媒質2の屈折率をn2とする。また、媒質1と媒質2の境界面に対し、媒質1からの入射角をθ、媒質2への出射角をξとする。

前編 (4)-⑦-2、(5)-⑦-2 で導出されたスネルの法則より、
ここで、媒質2を吸収のある媒質とする場合、(10)‐②と同様、屈折率n2を以下の複素屈折率で置き換えることで、媒質2による吸収の影響を数式で表すことができる。
このとき、(4),(5)-⑦-2 の右辺は実数なので、等式を満たすためにはξも複素数でなければならない。これを以下のように表すこととする。
ここで、各パラメータの値の範囲を以下のように定める。

(4),(5)-⑦-2のn2, ξをそれぞれ(11)-①-1,2で置き換え、式変形すると以下のようになる。
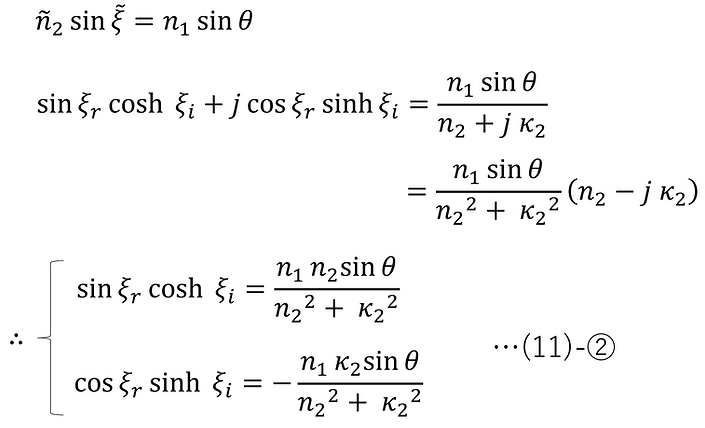
ここで、(11)-①-3 と (11)-② より、
[ i ] θ = 0 のとき、
ξr = ξi = 0
[ ii ] θ ≠ 0 のとき、
ξr ≠ 0 and ξi ≠ 0 となることから、
・ξi の導出:
(11)-②を式変形すると、

ここで、以下のようにおく。

これを上式に適用すると、
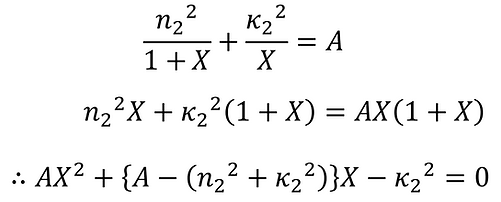
X > 0, A > 0 より、

ここで、以下のように置く。

これを上式に適用すると、

ここで、(11)-①-3 �と (11)-② より、以下のことが言える。

よって、

また、ξi は以下のように表すこともできる。
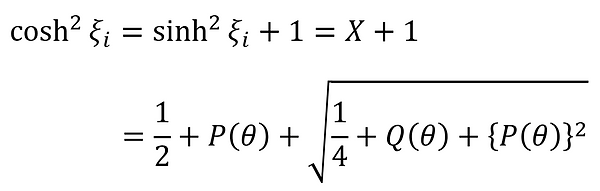
ここで、(11)-①-3 と (11)-② より、以下のことが言える。

よって、

但し、ξi < 0 (∵ (11)-③-5)
・ξr の導出:
改めて、(11)-②を式変形すると、

ここで、以下のよ��うに置く。

これと、前に示した (11)-③-1b を併せて、上式に適用すると、

Y > 0, A > 0 より、

ここでも、(11)-③-2a,b を適用すると、

ここで、(11)-①-3 より、以下のことが言える。

よって、

但し、0 < ξr < π/2 (∵ (11)-①-3)
また、ξr は以下のように表すこともできる。

ここで、(11)-①-3 より、以下のことが言える。

よって、

但し、0 < ξr < π/2 (∵ (11)-①-3)
・まとめ
以上の結果をまとめると、

… (11)-③-5,7, (11)-④-5,7

… (11)-③-2a,b
-
吸収がある媒質へのフレネルの公式の適用とエネルギー反射率
[ i ] θ=0のとき、
垂直入射においてはp偏光とs偏光は同じ状態なので、これらについてまとめて示す。
前編で導出した、垂直入射におけるフレネルの公式(s,p偏光)を改めて以下に示す。

ここで、屈折率n2を、(11)-①-1に示す複素数に置き換えることで、吸収がある媒質に入射する場合の振幅反射率(s,p偏光)を以下のように表すことができる。

よって、(6)-④,⑦より、吸収がある媒質に入射する場合のエネルギー反射率(s,p偏光)は以下のようになる。

[ ii ] θ≠0のとき、
・p偏光の場合
前編で導出したフレネルの公式(p偏光)を改めて以下に示す。

ここで、屈折率n2と出射角度ξを、(11)-①-1,2に示す複素数に置き換えることで、吸収がある媒質に入射する場合の振幅反射率(p偏光)を以下のように表すことができる。

よって、(6)-④より、吸収がある媒質に入射する場合のエネルギー反射率(p偏光)は以下のようになる。

但し、ξr と ξi は (11)-③-5,7, (11)-④-5,7 のθの関数で与えられるので、(12)-②-2もθの関数である。
ここで、振幅反射率(p偏光)rp は定義より以下のように入射光の電界振幅 Eip と反射光の電界振幅 Erp の比で表されるが、左辺を複素数に拡張しているので、右辺の電界の各振幅も複素数に拡張する必要がある。これを複素振幅と呼ぶ。

・s偏光の場合
前編で導出したフレネルの公式(s偏光)を改めて以下に示す。

ここで、屈折率n2と出射角度ξを、(11)-①-1,2に示す複素数に置き換えることで、吸収がある媒質に入射する場合の振幅反射率(s偏光)を以下のように表すことができる。
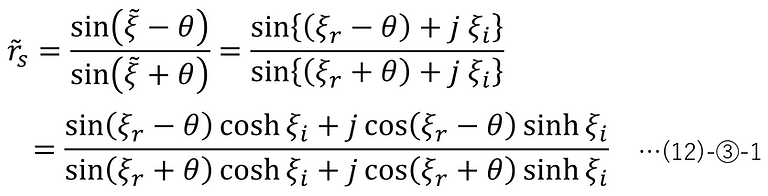
よって、(6)-⑦より、吸収がある媒質に入射する場合のエネルギー反射率(s偏光)は以下のようになる。

但し、ξr と ξi は (11)-③-5,7, (11)-④-5,7 のθの関数で与えられるので、(12)-③-2もθの関数である。
ここで、振幅反射率(s偏光)rs は定義より以下のように入射光の電界振幅 Eis と反射光の電界振幅 Ers の比で表されるが、左辺を複素数に拡張しているので、右辺の電界の各振幅も複素数に拡張する必要がある。これを複素振幅と呼ぶ。

・事例
波長589.3nmにおけるアルミニウムの屈折率を1.44、消光係数を5.23としたとき、空気からアルミニウムに入射したときの、入射角度θとエネルギー反射率の関係を、(12)-②,③-2を用いて計算すると、以下のグラフが得られる。

ここで注目すべき点としては、吸収のない媒質では、p偏光において、反射率が零となる角度のブリュースタ角があったが、吸収のある媒質では、反射率が零に落ちる角度がそもそもないので、反射率が零となる角度という意味でのブリュースタ角は定義できない。
-
エリプソメトリーの原理
ここまで、スネルの法則とフレネルの公式を複素数に拡張することで、吸収のある媒質へこれらの適用範囲を広げてきた。この原理を応用することで、薄膜の膜厚測定や、光学定数(屈折率、消衰係数など)、組成比、表面粗さ、結晶性など評価が可能になる。これを実現する分析技術のエリプソメトリーについて、基本原理の導出を示す。
・エリプソメトリーの定義式の導出
最初に、以下の値の範囲について調べる。

(11)-②より、

n2 > n1 とすると、
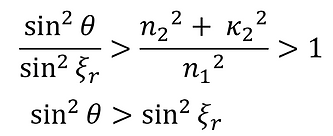
よって、(11)-①-3 より、

また、(11)-①-3 と (13)-②-1 より、

(13)-②-1,2,3 と、ξi < 0 (∵(11)-③-5) を踏まえ、n2 > n1 のとき、(12)-②-1と(12)-③-1は振幅と偏角を用いて以下のように表すことができる。


ここで、式中の青色の箇所は、θ+ξrの値がπ/2未満のときは零、π/2より大きいときは-πになるような場合分けを式中に組み入れたものである。
また、ξr と ξi は (11)-③-5,7, (11)-④-5,7 のθの関数で与えられる。
この結果を適用することで、エリプソメトリーで定義されるフレネル振幅反射係数比ρは、位相差Δと振幅比角ψ(これらをエリプソメトリーパラメータと呼ぶ)を用いて、以下のように表される。

但し、位相差Δの定義域を、0≤Δ≤2πとする。(13)-④-2の値がこれを外れた際には、2mπ(mは整数)を加算して定義域に入るようにmの値を選べばよい。
例として、n=1.44, κ=5.23 のとき、θを変数として ψ, Δを計算すると以下のようになる。


・吸収がある媒質におけるp,s偏光の電界ベクトルの記述
ここで、改めて電磁波の式について振り返る。入射光のp,s偏光の電界ベクトルをそれぞれEip, Eis、入射光のp,s偏光の電界振幅ベクトルをそれぞれEAip, EAis、入射光の波数ベクトルを ki としたとき、前章(2)-①より、これらの関係は以下のように表される。

ここで、入射光のp,s偏光の電界振幅ベクトルの単位ベクトルを以下のように定義する。

このとき、(13)-⑤-1,2は以下のように書き換わる。

同様に、反射光のp,s偏光の電界ベクトルをそれぞれErp, Ers、反射光のp,s偏光の電界振幅ベクトルをそれぞれEArp, EArs、反射光の波数ベクトルを kr としたとき、前編(2)-①より、これらの関係は以下のように表される。

ここで、反射光のp,s偏光の電界振幅ベクトルの単位ベクトルを以下のように定義する。

このとき、(12)-②-3, (12)-③-3 より、(13)-⑧-1,2は以下のように書き換わる。

・エリプソメトリーにおけるp,s偏光の電界ベクトルの記述と図示
ここで、エリプソメトリーにおいては、入射光を以下のように設定する。

このとき、(12)-②-3、(12)-③-3、(13)-④-1より、以下が成り立つ。

(13)-⑦-1,2は、(13)-⑪を適用すると以下のように書き換わる。

これは即ち、p軸(またはs軸)に対しπ/4(45°)だけ傾いた直線偏光である。この状態は、単色エリプソメトリーでは直線偏光のレーザを用いることで、また、分光エリプソメトリーでは白色光を偏光子に通すことで、実現できる。
また、(13)-⑩-1,2は、(13)-③の1,2 と (13)-④-2 と (13)-⑪ を適用すると、以下のように書き換わる。

よって、p偏光は時間軸で見た場合はs偏光に対しΔ/ω進んでいる。
以上を踏まえ、時間軸においてψとΔは以下のように図示できる。

ここで、入射光の電界については、(13)-⑪の条件に加え、絶対値を1に規格化して示した。
このように、直線偏光の入射光に対し、反射で位相差Δが生じることで、反射光は一般的に楕円偏光となる。
Δの値に応じて偏光は下図のように変化する。Δ=0,πでは直線偏光で、それ以外では楕円偏光となるが、Δ=0,πの前後で右回りと左回りの向きが反転する。

更に、(13)-⑭-1a,2a はそれぞれ、以下のように表すこともできる。
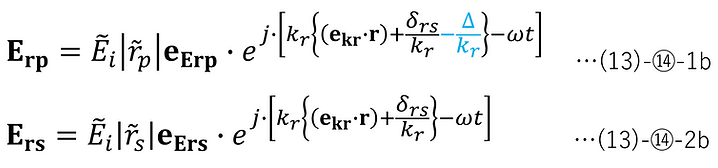
よって、p偏光は空間軸で見た場合はs偏光に対しΔ/kr遅れている。
以上を踏まえて、空間軸においてψとΔは以下のように図示できる。

ここでも、入射光の電界については、(13)-⑪の条件に加え、絶対値を1に規格化して示した。