電磁波に関する様々な公式の導出
(吸収がない媒質の場合)
※数式の参照があちこち飛ぶので、参照先の数式を見たりするときは、複製した別ウインドウで見ることをお勧めします。
電磁波に関する様々な公式を、以下の流れで体系的に導出をしていく。全体を流れで理解することをお勧めする。
-
パラメータの定義と関係式
まず、電磁波の各パラメータの定義について示す。

ここで、真空中の誘電率・透磁率は以下の定数である。

定義に基づく、各パラメータとパラメータ間の関係について示していく。
・光速は光が単位時間に進む距離であり、波長は光が一回振動する間に進む距離である。また、周波数は単位時間に光が振動する回数である。よって周波数は、光速を波長で割った値で表される。また、角周波数は周波数を位相で表したものである。

・波数は、単位長さで光が振動する回数を位相で表した量である。よって波長は、単位長さを波数で割り、2πを掛けた値で表される。
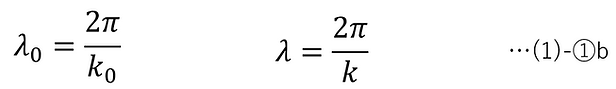
・特性インピーダンスは、伝送媒体(伝送線路や空間)を伝わる電磁波の電場と磁場の比率である。

・屈折率は、真空中の光速と媒質中の光速の比であり、媒質固有の値を持つ。また、屈折率の値は(メタマテリアル等の特殊なケースを除き)常に1以上の値である。

誘電率・透磁率と各パラメータの関係は、マクスウェルの方程式[1]より導出され、その結果は以下のようになる。
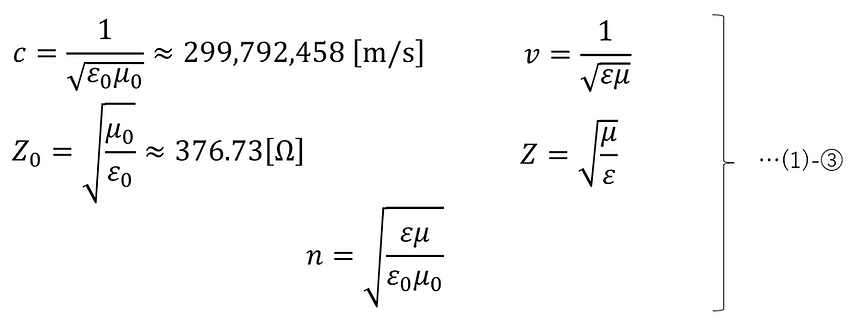
また、真空中と媒質中の角周波数��の間には以下の関係がある ( この関係は(3)-⑥で導出される )。
(3)-⑥を(1)-①に適用し、更に(1)-③をこれと統合して整理すると、以下の関係式が得られる。

また、非磁性の媒質では、透磁率は以下のように扱える。

このとき、(1)-④は更に以下のように書き換えられる。

(1)-④と(1)-⑥はそれぞれ、磁性・非磁性の媒質における電磁波の各パラメータの関係を示す式として、非常に重要である。
-
電磁波の数式表現
電磁波は、以下のように表すことができる(マクスウェルの方程式から導出された結果のみ示す)[2]。
電界ベクトル:
磁界ベクトル:

電界と磁界の関係は以下で表される。
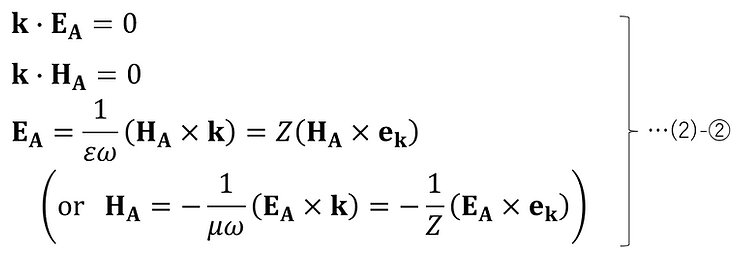
ここで、各ベクトル��は以下で定義された量である。

また、(2)-②の第3式の中で、(1)-④から導かれる以下の関係を用いている。

(2)-②に示すベクトルの向きの関係を図示すると以下のようになる。
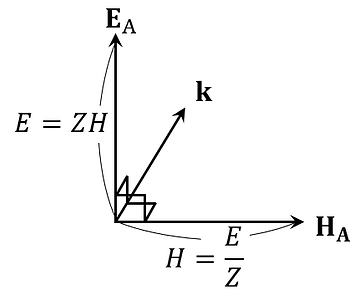
ここで、ベクトルの奥行き方法は以下のように表示できる。
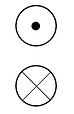
…奥から手前へ
…手前から奥へ
これを用いると、(2)-②に示すベクトルの向きの関係は次のように表記できる。
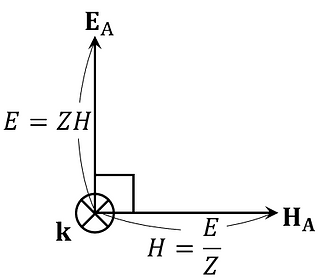
(2)-①で表される電磁波を図示すると、以下のようになる。ここで、図を煩雑にしないため、ekz=0としたが、ekzが0でない場合についても同様に考えることができる。

また、位相の進みと電磁波の進みの関係について図示すると、以下のようになる。
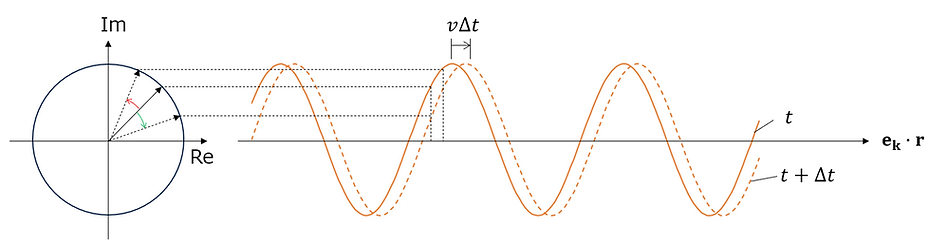
このように、位置の進みと時間の進みで、位相が逆向きになっているため、位置成分と時間成分で、符号が反対となる。
-
媒質間の伝搬における境界条件
以下の図に示すように、非磁性の媒質間の光の伝搬において、z=0平面を媒質間の境界面とし、電磁波が境界面に入射したときの、透過光と反射光について考える。

ここで、各パラメータの下付き添え文字は以下を意味する。
i : 入射光における値
r : 反射光における値
t : 透過光における値
入射光、反射光、透過光の電界と磁界は、(2)-①より以下のように表される。
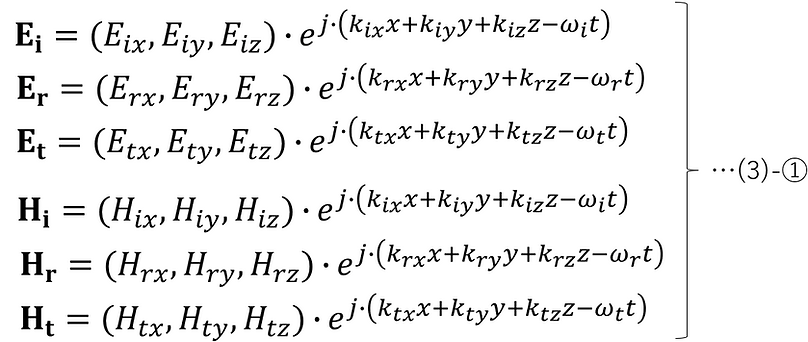
ここで、境界面における電磁場の境界条件を考える。
z=0で電界の接線成分が連続となることより、
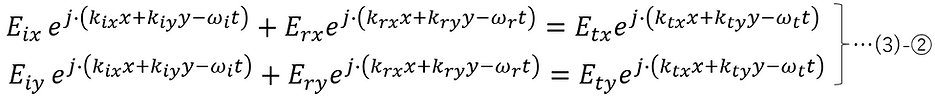
z=0で磁界の接線成分が連続となることより、

任意のx, y, t に対して(3)-②、(3)-③が成り立つための条件は、

このとき、(3)-②、(3)-③は以下のようになる。
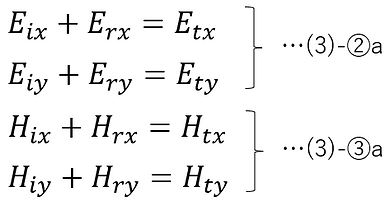
(3)-④-3より、入射光・反射光・出射光のωは、下付き添え文字を外した共通のωで表すこととする。
また、このωは媒質に依存しないことから、以下のことも言える。
ここで、𝑘𝑖𝑦=0となる方向にy軸を決めても一般性を失わない。
このとき、(3)-④-1より、以下のようになる。
このことから、 𝑘𝑖𝑦=0となる方向にy軸を決めた場合、入射光・反射光・透過光は全てxz平面内にあることが言える。
また、電界・磁界はそれぞれ、入射面に対して平行に振動する成分(p偏光)と、入射面に対して垂直に振動する成分(s偏光)の和で表すことができるので、次の章ではこれらを分けて考えることとする。
-
p偏光におけるフレネルの公式
z=0平面の媒質の境界面への入射において、電界が入射面に対して平行に振動する場合(p偏光)について考える。このとき、入射光・反射光・透過光の電界・磁界は下図のように表される。

下付き添え字の1,2はそれぞれ媒質の違いを表す。
電界と磁界の向きは、(2)-②に従って図示されている。
非磁性の吸収のない媒質間の伝搬とし、(1)-⑥が適用できるものとする。
図に示されている各ベクトルを成分表示で示すと、以下のようになる。
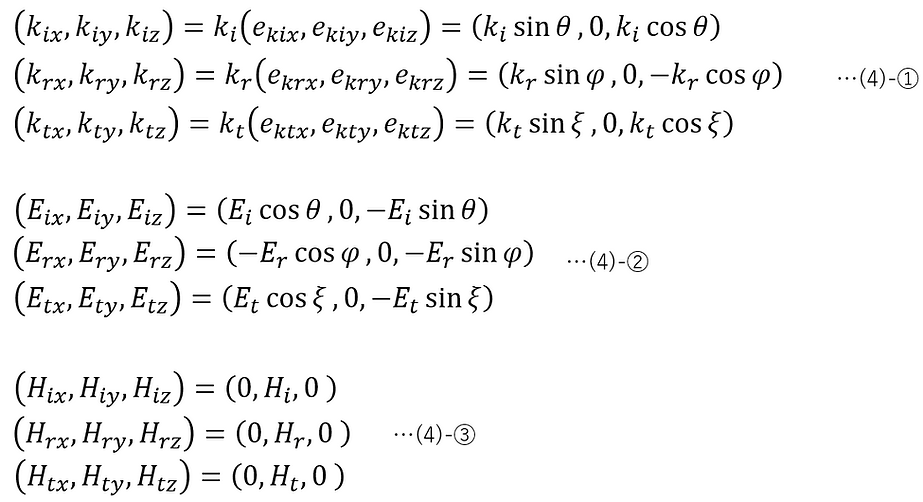
ここで、(1)-⑥より、

(4)-④-1より、

また、(3)-④-1(境界条件の解)、(4)-①(p偏光における波数の成分表示)より、

(4)-⑤、(4)-⑥より、以下の反射の法則とスネルの法則が求められる。

(4)-②③(p偏光における電界・磁界の成分表示)を(3)-②a, ③a(電界・磁界の振幅の境界条件) へ代入する。その際に、(4)-④-2(電界と磁界の振幅の関係式)と(4)-⑦-1(反射の法則)を適用すると以下が得られる。
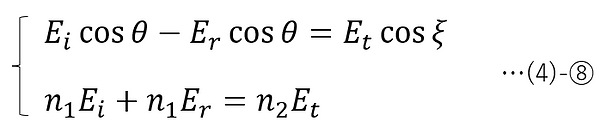
よって、振幅透過率をtp、振幅反射率をrpとすると、以下のフレネルの公式(p偏光)が求められる。

ξ≠0のとき、(4)-⑨は更に、(4)-⑦-2を適用して以下のように表すこともできる。
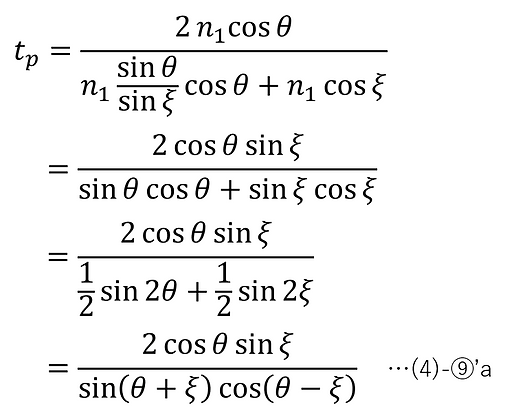

θ=0のとき、(4)-⑦-2よりξ=0となり、このとき、(4)-⑨より、

-
s偏光におけるフレネルの公式
z=0平面の媒質の境界面への入射において、電界が入射面に対して垂直に振動する場合(s偏光)について考える。このとき、入射光・反射光・透過光の電界・磁界は下図のように表される。

下付き添え字の1,2はそれぞれ媒質の違いを表す。
電界と磁界の向きは、(2)-②に従って図示されている。
非磁性の吸収のない媒質間の伝搬とし、(1)-⑥が適用できるものとする。
図に示されている各ベクトルを成分表示で示すと、以下のようになる。
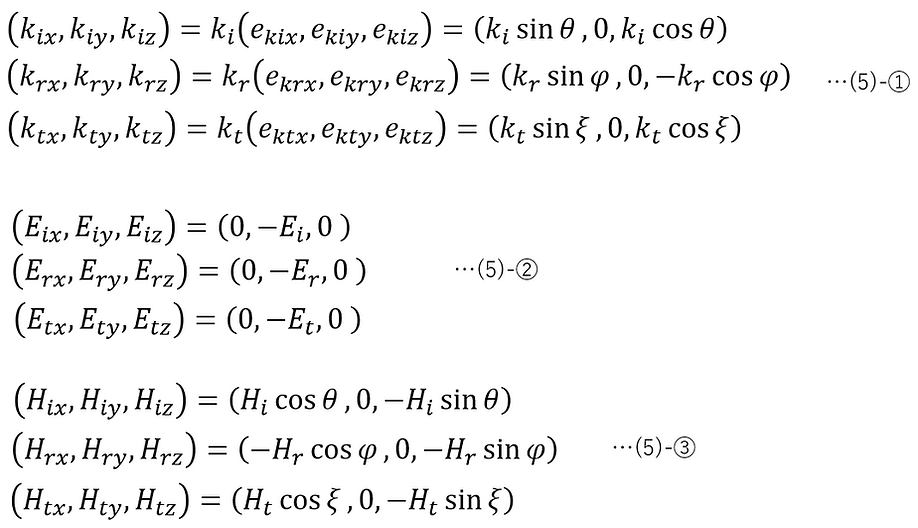
ここで、(1)-⑥より、
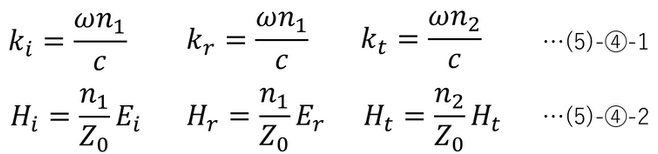
(5)-④-1より、

また、(3)-④-1(境界条件の解)、(5)-①(s偏光における波数の成分表示)より、

(5)-⑤、(5)-⑥より、以下の反射の法則とスネルの法則が求められる。

(5)-②③(s偏光における電界・磁界の成分表示)を(3)-②a, ③a(電界・磁界の振幅の境界条件) へ代入する。その際に、(5)-④-2(電界と磁界の振幅の関係式)と(5)-⑦-1(反射の法則)を適用すると以下が得られる。
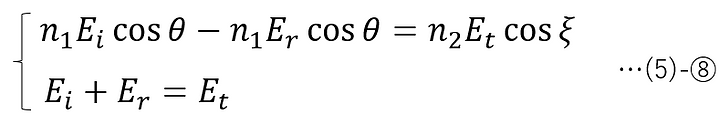
よって、振幅透過率をts、振幅反射率をrsとすると、以下のフレネルの公式(s偏光)が求められる。

ξ≠0のとき、(5)-⑨は更に、(5)-⑦-2を適用して以下のように表すこともできる。


θ=0のとき、(5)-⑦-2よりξ=0となり、このとき、(5)-⑨より、
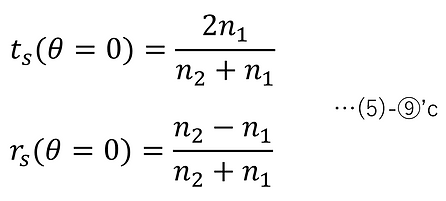
p偏光の垂直入射とs偏光の垂直入射は同じ状態なので、当然ながら(4)-⑨'cと(5)-⑨'cは同じ式となる。
-
エネルギー透過率とエネルギー反射率
z=0平面上の微小領域dxdyを単位時間に通過する入射光・反射光・透過光の体積をそれぞれdVi、dVr、dVtとする。これらを図示すると以下のようになる。
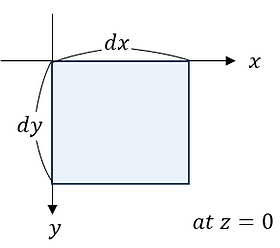
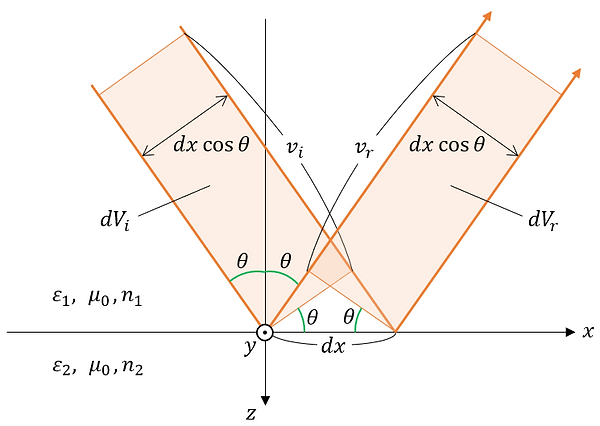
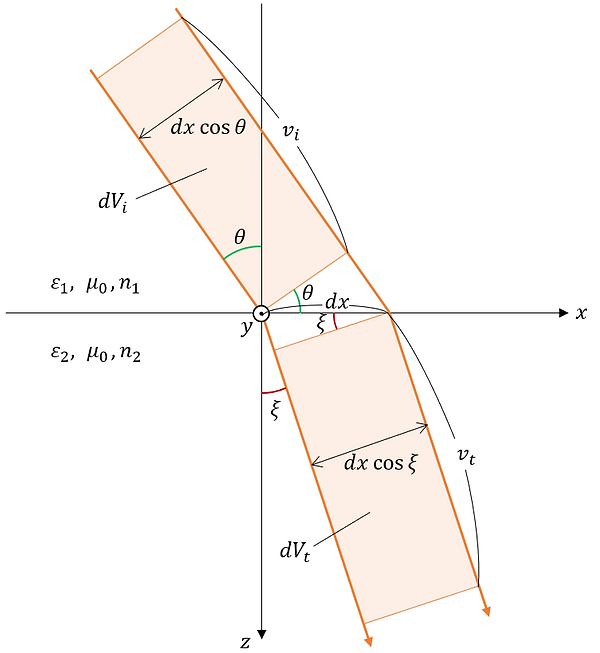
図より、dVi, dVr, dVt は以下のように表される。

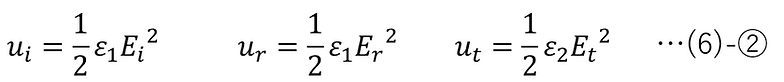
よって、(6)-①,②と(1)-⑥より、z=0平面上の微小領域dxdyを単位時間に通過する入射光、反射光、透過光のエネルギー量はそれぞれ以下のように表すことができる。
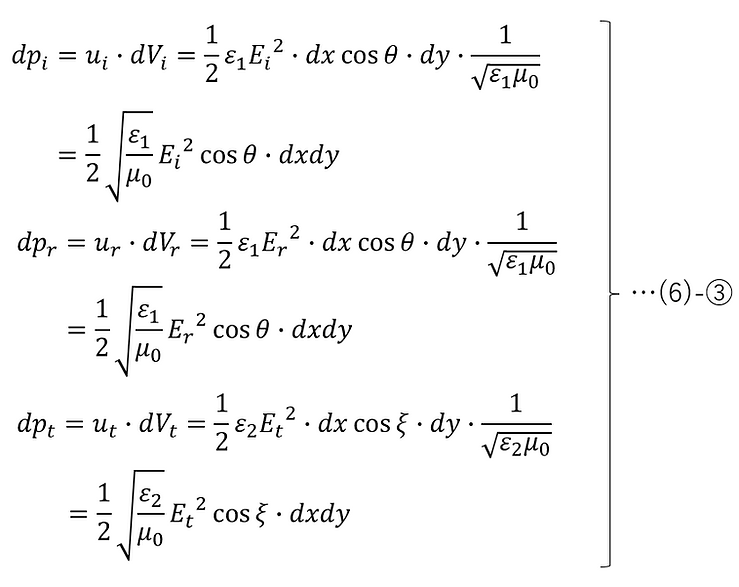
よって、p偏光のエネルギー透過率 Tp とエネルギー反射率 Rp はそれぞれ以下のようになる。
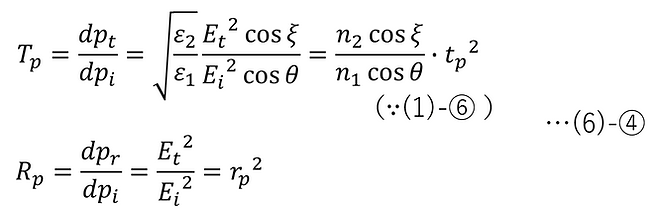
これに(4)-⑨を代入すると、

(6)-④’より、以下の計算結果から、エネルギー保存則を満たしていることを確認できる。
垂直入射では、以下のようになる。
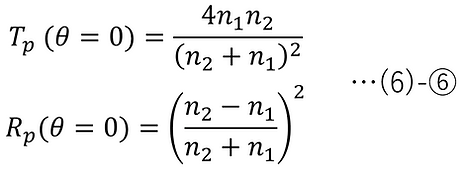
また、s偏光のエネルギー透過率 Ts とエネルギー反射率 Rs はそれぞれ以下のようになる。

これに(5)-⑨を代入すると、

(6)-⑦’より、以下の計算結果からエネルギー保存則を満たしていることを確認できる。
垂直入射では以下のようになる。p偏光の垂直入射とs偏光の垂直入射は同じ状態なので、当然ながら(6)-⑥と(6)-⑨は同じ式となる。
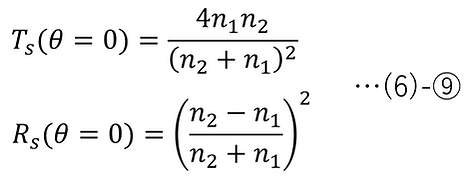
n1=1, n2=2の場合について、(4)-⑨、(5)-⑨、(6)-④'、(6)-⑦'をグラフにすると以下のようになる。


n1>n2のときはθを大きくしていくと全反射が起こるので、これについては後に示す。
-
ブリュースター角
前章で示した、エネルギー反射率の入射角度依存性のグラフから判るように、p偏光はある入射角度において反射がなくなる。この角度をブリュースター角θBと言い、これを導出していく。
(4)-⑨において、rp=0となるとき、

(4)-⑦-2(スネルの法則)より、
(7)-①,②より、
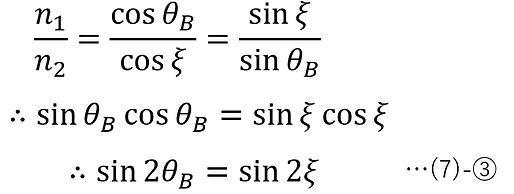
ここで、以下の角度条件を考慮する。

このとき得られる解は、以下である。
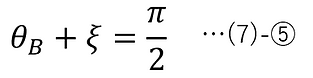
再度、(4)-⑦-2(スネルの法則)より、

-
全反射とエバネッセント波
n1>n2のとき、入射光の角度を大きくしていくと、ある入射角度θで、透過光の出射角 ξ はπ/2となる。このときの入射角を臨界角と言い、(4)-⑦-2、(5)-⑦-2(スネルの法則)より、p偏光・s偏光の何れにおいても以下となる。

これよりも大きい入射角度においてはスネルの法則は実数解 ξ を持たない。このとき、入射光はすべて反射する。このことを全反射と呼ぶ。n1>n2のときのエネルギー透過率・反射率の入射角度依存性は以下のようになる。

また、全反射条件においても、ξを複素数に拡張すると、スネルの法則は解を持つことができる。即ち、全反射条件では、 sinξは1以上の実数値となるが、このときのξは複素数である。
全反射条件における複素数解は以下のように求めることができる。
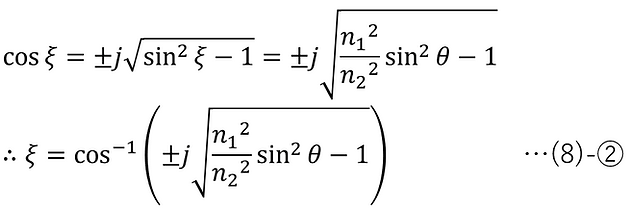
p偏光においては、全反射条件における透過光の電界・磁界は、(4)-①,②,③を(3)-①へ代入して、(8)-②, (4)-④-2, (4)-⑤-2, (4)-⑥, (4)-⑦-2 を適用すると以下が得られる。

s偏光においては、全反射条件における透過光の電界・磁界は、(5)-①,②,③を(3)-①へ代入して、(8)-②, (5)-④-2, (5)-⑤-2, (5)-⑥, (5)-⑦-2を適用すると以下が得られる。
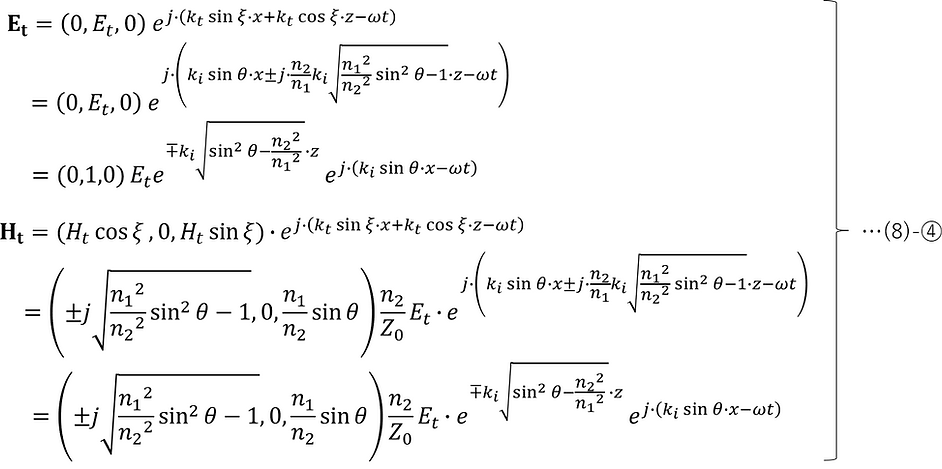
求めた結果はあくまで、数学的に得られた解であるが、p偏光・s偏光のどちらにも共通する以下のzに依存する成分の内、複号のマイナスについては、物理的に実際に存在するエバネッセント波を表す(複号のプラスは物理的には存在しない)。
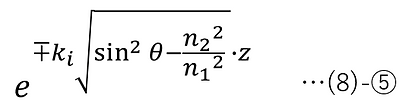
これはzに対し指数関数的に振幅が減衰していくことを意味し、振幅が1/e倍に減衰するまでの界面(z=0)からの距離(染み出し深さ)は以下で表される(式変形で③-⑧を適用)。

エバネッセント波の染み出しが反射光の光量(エネルギー反射率)に及ぼす影響については、(8)-②を(6)-④,⑦へ代入するとRp=1, Rs=1となるので全反射で光量ロスがないことが判る。但し、Tpについては(6)-④,⑦の代入で値が零にならず、Tsについては分母が零になってしまって計算ができない。これは、TpとTsは式の導出過程でエバネッセント光を想定していないためである。
-
ストークスの関係式
(4)-⑨と(5)-⑨で、媒質1から媒質2に入射するときのp偏光・s偏光の振幅反射率をそれぞれrp, rs、振幅透過率をぞれぞれtp, tsとした。ここから示すことはp偏光とs偏光のどちらについても成り立つので、p,sの下付き添え文字を省略し、振幅反射率をr、振幅透過率をtとして表す。
また、反対側の媒質2から媒質1に入射するときの振幅反射率をr’、振幅透過率をt’とする。
媒質1と媒質2のどちらも吸収がないとする。
このとき、まず、以下の図9-1の電界振幅の関係が成り立つ。

次に、図9-1の反射光を逆方向にして再び界面に入射させると、以下の図9-2の電界振幅の関係が成り立つ。
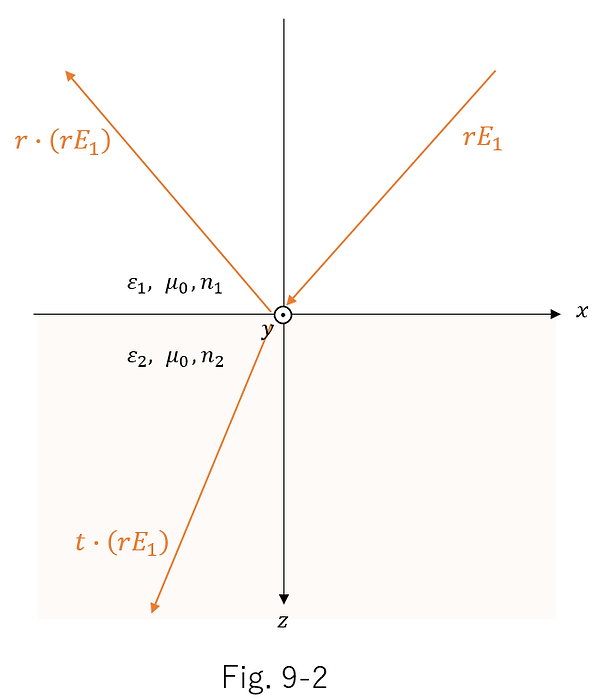
更に、図9-1の透過光を逆方向にして再び界面に入射させると、以下の図9-3の電界振幅の関係が成り立つ。
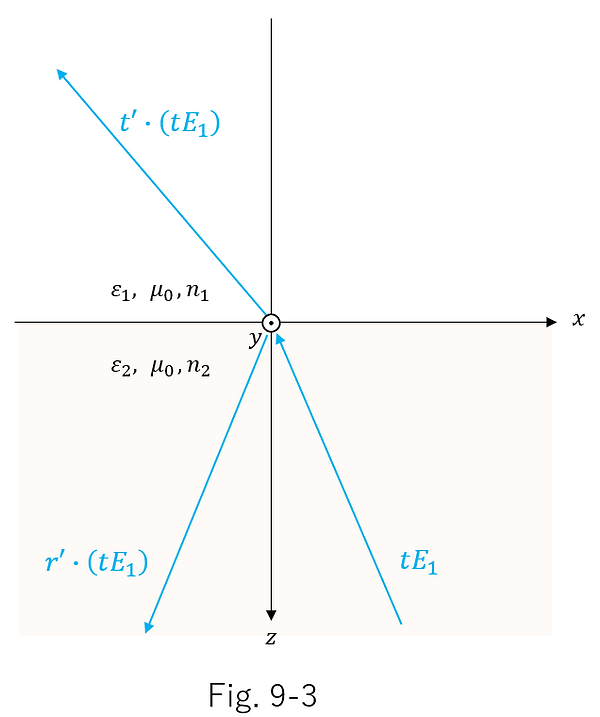
また、媒質での吸収がない場合は、光波の進行は可逆的であることから、図9-1の入射光・反射光・透過光の全ての進行を反対方向にした、以下の図9-4も成り立つ。
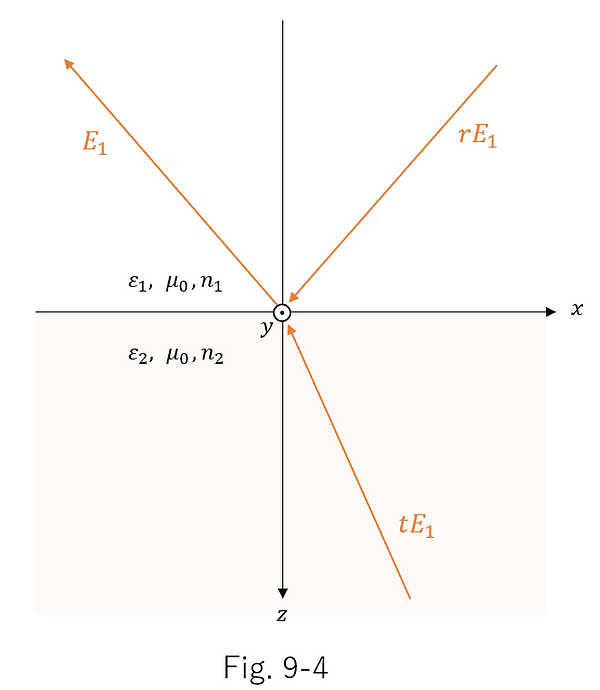
ここで、図9-2, 9-3 を合成した以下の図9-5は、図9-4と入射光が同じである。ということは、透過・反射光も同じになるはずである。

このことから、以下の等式が成り立つ。
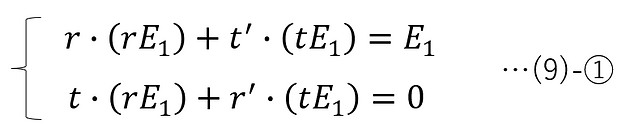
即ち、
