スネルの法則から導かれる
平行平面板における関係式
光線の物質界面での屈折の法則(スネルの法則)から、様々な関係式を導くことができる。ここでは、実用的なものをいくつか紹介する。
-
平行平面板に垂直に入射した収束光の結像位置
実像が平行平面板の中にある場合と、平行平面を出た先にある場合の、2通りに分けて、虚像に対する実像の位置について求める。

(1) 実像が平行平面板中にある場合:

※寸法表記については、付録:1次元ベクトルと角度の方向と符号の定義について を参照
ここで、dhとdθ1とdθ2は微小量とする。
図に示されている条件を式で表すと、以下のようになる。

ここで、2番目の式はスネルの法則である。また、dθ1とdθ2は微小量であるから、以下のことが言え��る。

よって、元の式は以下のように置き換えられる。

これを解くと、以下が導出される。

(2) 実像が平行平面板を出た先にある場合:

※寸法表記については、付録:1次元ベクトルと角度の方向�と符号の定義について を参照
ここで、dhとdθ1とdθ2は微小量とする。
図に示されている条件を式で表すと、以下のようになる。

ここで、2番目の式はスネルの法則である。また、dθ1とdθ2は微小量であるから、以下のことが言える。

よって、元の式は以下のように置き換えられる。

これを解くと、以下が導出される。

-
平行平面板を光軸に対し斜めに配置したときの結像位置
以下のように平行平面板に斜めに入射して、出射した先で結像する光束を考える。このときのΔxとΔyを求める。

ここで、dh、dθ1、dθ2は微小量とする。
図に示されている条件を式で表すと、

ここで、④の立式について触れておく。dθ1とdθ2は微小量であることから、赤線と緑点線は平行であるとみなすと、以下のように、境界面に入射前の光線幅は、境界面を通った後の光線幅に対し、cosθ1/cosθ2倍になるので、このことを加味して④を立式した。

③の両辺を微分して、

①、②、③’、④、⑤より、s, xA, xB, x0, dh, dθ1, dθ2を消去すると、

ここで、①、⑥より、
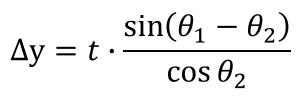
また、③より、
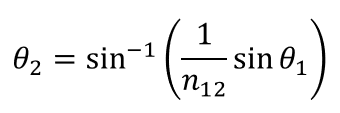
よって、求める解は以下のように表すことができる。

更に、③を適用してθ2を消去すると、


ここで具体例として、θ1=45[deg], n=1.5とすると、��以下のようになる。

-
平行平面板で発生する球面収差量
以下の光学配置について考える。

dθ1とdθ2は微小量とし、縦方向球面収差 δs、横方向球面収差 δx について求めていく。
図に示されている条件を式で表すと、以下のようになる。

①と③はスネルの法則、⑤は開口数を表す。
①、②、⑤より、

③、④より、

②'、④'より、縦方向球面収差は以下のようになる。

⑥、⑦より、横方向球面収差は以下のようになる。

球面収差量を図示すると以下のようになる。図から判るように、同じ板厚に対しては比屈折率が1.6辺りで、球面収差量がピークになる。


ここで、収差の影響について考察する。
波動光学的な回折広がりによる点像分解能(エアリーディスク半径)は、以下の式で表される。

あくまで大まかな目安であるが、δxがδdよりも十分に小さいときには、δdが分解能において支配的となるため、δxの影響は小さいと言える。一方で、δxがδdよりも十分に大きいときは、δxが分解能において支配的となる。
δxとδdの比較のグラフを以下に示す。あくまで大まかな目安であるが、波長532nmでは、カバーガラス(厚さ約0.15mm程度)においてはNA0.32以上、厚さ1.5ミリのガラスにおいてはNA0.18以上で、回折広がりの点像分解能よりも球面収差の影響が支配的になり、また、波長1064nmでは、カバーガラス(厚さ約0.15mm程度)においてはNA0.38以上、厚さ1.5ミリのガラスにおいてはNA0.22以上で、回折広がりの点像分解能よりも球面収差の影響が支配的になる。
