Astigmatism of a spherical mirror caused by oblique ray incidence and its correction

Consider a system in which light is reflected obliquely by a spherical mirror as shown below. In this case, the focal length in the sagittal direction (red line) is r/(2cosθ), and the focal length in the tangential direction (blue line) is (r cosθ)/2 (in the paraxial region), resulting in large astigmatism.

This shows the astigmatism that occurs when light is obliquely incident on a spherical mirror.

Below, we will consider the reasons for this.

table of contents:

Derivation of the focal length of the tangential component

Derivation of the focal length of the sagittal component

Toroidal surface shape for astigmatism correction

Derivation of the focal length of the tangential component

First, as shown below, consider only the tangential component in a system where light is reflected obliquely by a spherical mirror.

Here, dθ and dψ are assumed to be infinitesimal quantities, and cos dθ = 1 and sin dθ = dθ are assumed to hold.

The conditions shown in the figure can be expressed as follows:

Astigmatism caused by oblique incidence on a spherical mirror_102.png

From Law of Sines,

Therefore, it was shown that the focal length in the tangential direction is (r cos θ)/2.

Derivation of the focal length of the sagittal component

Next, as shown below, consider only the sagittal component in a system where light is reflected obliquely by a mirror.

Sagittal component of a ray of light incident obliquely on a spherical mirror

Here, vector i is the direction vector of the incident light, vector j is the direction vector of the reflected light, and vector n is the normal vector of the reflecting surface.

The angle dφ is assumed to be very small.

Each direction vector is expressed as follows:

Direction vectors of incident and reflected light, and normal vector of the reflecting surface

Substituting ① and ② into ③,

Astigmatism occurring when light is incident obliquely onto a spherical mirror_213.png

Moreover, the vectors between each point are expressed as follows:

Astigmatism occurring when light is incident obliquely onto a spherical mirror_214.png

Here, k is a positive real number,

If we substitute ③' and ⑥ into this and compare the y components, we get

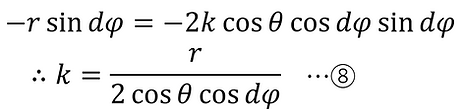
Astigmatism occurring when light is incident obliquely onto a spherical mirror_216.png

Substituting ③' and ⑧ into ⑦, we get

Astigmatism occurring when light is incident obliquely onto a spherical mirror_215.png

Compare this with ⑥

Astigmatism occurring when light is incident obliquely onto a spherical mirror_217.png

Therefore, from ⑤,

Astigmatism occurring when light is incident obliquely onto a spherical mirror_218.png

Here, since d𝜑 is an infinitesimal quantity, cos⁡ d𝜑 ≅ 1,

This is the result of calculating the focal length in the sagittal direction.

Therefore, it was shown that the focal length in sagittal direction is r/(2cosθ).

Toroidal surface shape for astigmatism correction

So far, we have treated the reflecting surface as a spherical surface, but here we consider a toroidal surface, which has a shape with different radii of curvature in the tangential and sagittal directions.

The toroidal surface can be illustrated as follows:

Diagram of the shape of a toroidal mirror

In this case, the shape of the toroidal surface can be expressed by the following formula [1] [2]:

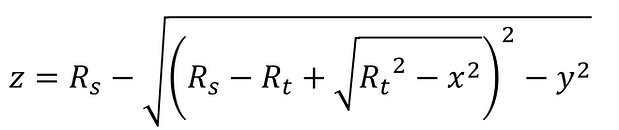
Formula for the shape of a toroidal mirror

where:

Tangential radius of curvature: R t = r/cosθ

Sagittal radius of curvature: R s = r cosθ

Then, the focal length in both the tangential and sagittal directions is r/2, which is the same, and astigmatism can be eliminated.

However, the aberration that occurs when light is incident obliquely on a spherical mirror is not just astigmatism; coma aberration also becomes a problem. One way to correct this is to use multiple mirrors to cancel out the coma aberration that occurs in each mirror. Czerny-Turner spectrometers are designed based on this concept.

Related Topics

The vector relationships between incident light, reflected light, and the normal are derived in detail at the following link.

Vector representation of ray reflection and refraction at material interfaces

We have discussed astigmatism of reflected light caused by oblique incidence onto a mirror, and a similar phenomenon, astigmatism of refracted light caused by oblique incidence onto a parallel plane, is also discussed below.

Ray Propagation and Aberrations in a Plane‑Parallel Plate: A Theoretical Analysis Based on Snell’s Law