top of page

Vector representation of reflection and refraction of light at material interfaces

Expressing the reflection of light at the interface of a material and the refraction of light based on Snell's law as vectors is extremely useful when dealing geometrically with the propagation of light. Here, we will derive it.

  • Vector representation of reflection at material interfaces

Each direction vector is defined as follows.

The diagram shows the direction vector of the incident light, the direction vector of the reflected light, and the normal vector of the reflecting surface for the reflection of a light ray at an interface.

where:

Vector i: Direction vector of incident light
Vector i': Direction vector of reflected light
Vector e: Normal vector of the reflecting surface

The absolute values of all these are defined as 1.

In this case, k can be expressed as follows, where k is a positive real number.

Mirror reflection vector notation_014.PNG

Transforming this into the formula,

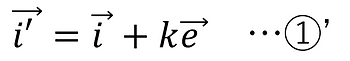
Mirror reflection vector notation_015.PNG

Squaring both sides,

Mirror reflection vector notation_016.PNG

Since the absolute value of each direction vector and normal vector is 1,

Mirror reflection vector notation_017.PNG

By substituting this into ①', we finally get the following equation.

Mirror reflection vector notation_022.png

Next, we will show how to calculate the direction vector of a ray after it has reflected off multiple boundary surfaces. The reflection off the j-th boundary surface is illustrated as follows:

The recurrence model of the reflection of a ray at an interface shows the direction vector of the incident light, the direction vector of the reflected light, and the normal vector of the reflecting surface.

As shown in the figure, the light reflected from the jth boundary surface becomes incident light on the next surface, so by using the derivation result obtained in ②, the following recurrence formula can be obtained, and the direction vector of the light ray after reflecting off multiple reflecting surfaces can be finally determined.

Recurrence formula for vector representation of reflected light at material interfaces

Here, the components of each vector are set as follows:

Vector representation of Snell's law_023.png

In this case, ③ can be expressed as follows:

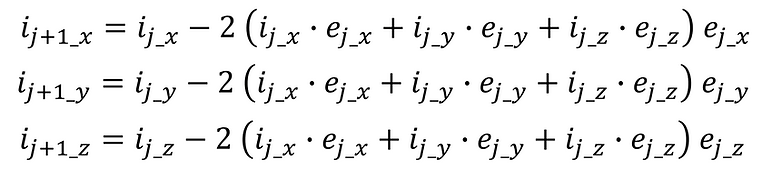
The recurrence formula for the vector representation of reflected light at a material interface is shown separated into components in each direction.

  • Vector representation of refraction at material interfaces

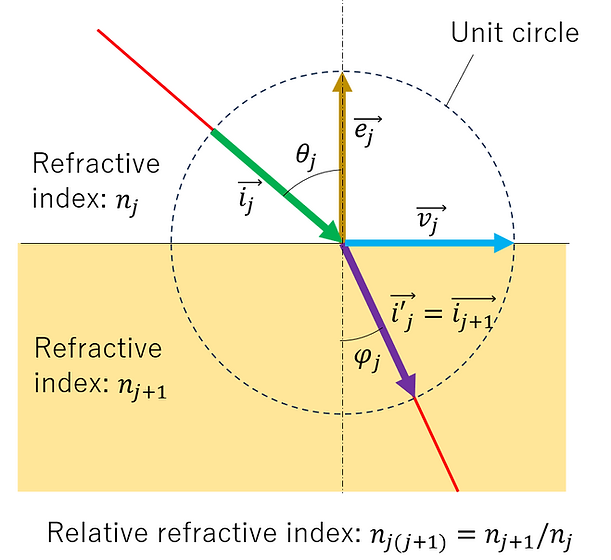
Define a direction vector as shown in the following diagram.

The diagram shows the refraction of light rays at an interface, with the direction vector of the incident light, the direction vector of the transmitted light, and the normal vector of the material interface.

where:

Vector i: Direction vector of incident light

Vector i': direction vector of transmitted light

Vector e: Normal vector of material interface

Vector v: A direction vector parallel to the material interface and in the same plane as the incident and transmitted light

The absolute values of all of these are set to 1.

In this case, the relationship between the vectors can be described as follows:

Vector representation of Snell's law_019.png

From ①,

Vector representation of Snell's law_011.PNG

Substituting ② and ③ into this,

Vector representation of Snell's law_012.PNG

Next, substitute ① and ③ into ⑤,

Vector representation of Snell's law_013.PNG

Substituting ④ into this,

Vector representation of Snell's law_014.PNG

By substituting ①' and ② into this, we finally obtain the following equation.

Vector representation of Snell's law_022.png

Next, let us consider the case where light passes through multiple boundary surfaces. The refraction at the j-th boundary surface is illustrated as follows:

The recurrence model of the refraction of light at an interface shows the direction vector of the incident light, the direction vector of the transmitted light, and the normal vector of the material interface.

As shown in the figure, the light transmitted through the jth boundary surface becomes the light incident on the next surface. Therefore, using the derivation result obtained in ⑥, the following recurrence formula is obtained, and the direction vector of the light ray after passing through multiple transmitting surfaces can be finally determined.

Recurrence formula for Snell's law in vector notation

Here, the components of each vector are set as follows:

Vector representation of Snell's law_023.png

In this case, ⑦ can be expressed as follows:

The vector representation of Snell's law is shown separated into components for each direction.
bottom of page