球面ミラーへ斜め入射で
発生する非点収差とその補正

　以下に示すような、球面ミラーで斜めに反射する系を考える。このとき、（近軸領域において）サジタル方向（赤線）の焦点距離はr/(2cosθ)、タンジェンシャル方向（青線）の焦点距離は(r cosθ)/2となるため、大きな非点収差が発生する。

以下では、その理由について考察していく。

まず、以下に示すように、球面ミラーで斜めに反射する系においてタンジェンシャル成分のみを考える。

ここで、dθ、dψは微小量とし、cos dθ = 1, sin dθ = dθ が成り立つものとする。

図に示されている条件を式で表すと、

正弦定理より、

よって、タンジェンシャル方向の焦点距離が(r cosθ)/2であることが示された。

　次に、以下に示すように、ミラーで斜めに反射する系においてサジタル成分のみを考える。

ここで、ベクトル i は入射光の方向ベクトル、ベクトル j は反射光の方向ベクトル、ベクトル n は反射面の法線ベクトルである。

また、角度dφは微小量とする。

各方向ベクトル・法線ベクトルは以下のように表される。

①と②を③へ代入して、

また、各点間のベクトルは以下のように表される。

ここで、kを正の実数として、

と表されるので、これに③’と⑥を代入してy成分を比較すると、

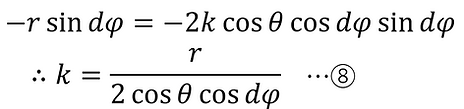
③’と⑧を⑦へ代入すると、

これと⑥を比較して

よって、⑤より、

ここで、d𝜑は微小量であることから、cos⁡ d𝜑≅1より、

よって、サジタル方向の焦点距離が r/(2cosθ) であることが示された。

これまでは反射面を球面形状として扱ってきたが、ここでは、タンジェンシャル方向とサジタル方向で曲率半径の異なる形状であるトロイダル面について考える。

トロイダル面を図示すると以下のように表される。

このとき、トロイダル面の形状は以下の数式で表すことができる[1] [2]。

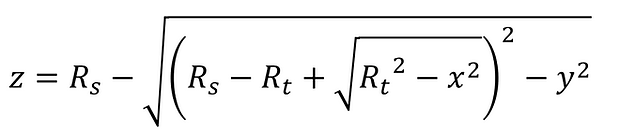
ここで、

タンジェンシャル方向の曲率半径：　Rt = r/cosθ

サジタル方向の曲率半径：　Rs = r cosθ

とすると、タンジェンシャル方向・サジタル方向のいずれも、焦点距離は r/2 となり、一致するので、非点収差をなくすことができる。

但し、球面ミラーに斜め入射させるときに発生する収差は非点収差だけではなく、実際にはコマ収差も問題となる。これを補正する方法としては、複数のミラーを用いて、各ミラーで発生するコマ収差を互いに打ち消す方法が考えられる。ツェルニターナー型分光器はこの考え方に基づいて設計されている。

タンジェンシャル成分の焦点距離の導出