光線の物質界面での
反射・屈折のベクトル表記
物質界面での光線の反射や、スネルの法則に基づく光線の屈折を、ベクトルで表記することは、光の伝搬を幾何学的に扱う際に、非常に有益となる。ここでは、その導出をしていく。
-
物質界面での反射のベクトル表記
各方向ベクトルを以下のように定義する。

ここで、
ベクトル i:入射光の方向ベクトル
ベクトル i':反射光の方向ベクトル
ベクトル e:反射面の法線ベクトル
これら全ての絶対値を1と定義する。
このとき、kを正の実数として、次のように表すことができる。

これを式変形して、
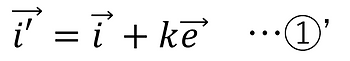
両辺を二乗して、

各方向ベクトル・法線ベクトルの絶対値は1であることから、

これを①'へ代入すると、最終的に以下の式が得られる。

次に、複数の境界面を反射する場合について示す。第 j 番目の境界面での反射を図示すると以下のようになる。

図に示されているように、第 j 番目の境界面での反射光は、その次の面への入射光となるので、②で得られた導出結果を用いて、以下の漸化式が得られるので、複数の反射面を反射した後の光線の方向ベクトルを最終的に求めることができる。

ここで、各ベクトルの成分を以下のように置く。

このとき、③は以下のように表すことができる。
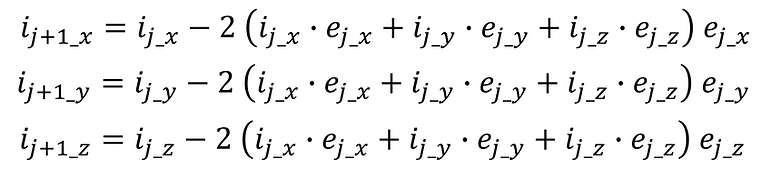
-
物質界面での屈折のベクトル表記
以下の図に示すように、方向ベクトルを定義する。

ここで、
ベクトル i :入射光の方向ベクトル
ベクトル i':透過光の方向ベクトル
ベクトル e:物質界面の法線ベクトル
ベクトル v:物質界面に平行且つ入射・透過光と同一平面内にある方向ベクトル
これら全ての絶対値を1とする。
このとき、各ベクトルの関係を以下のように記述できる。

ここで、①はスネルの法則を表す。
①より、

これに②と③を代入して、

次に、⑤に①と③を代入して、

これに④を代入して、

これに①’と②を代入して、最終的に次式が得られる。

次に、複数の境界面を透過する場合について考える。第 j 番目の境界面での屈折を図示すると以下のようになる。
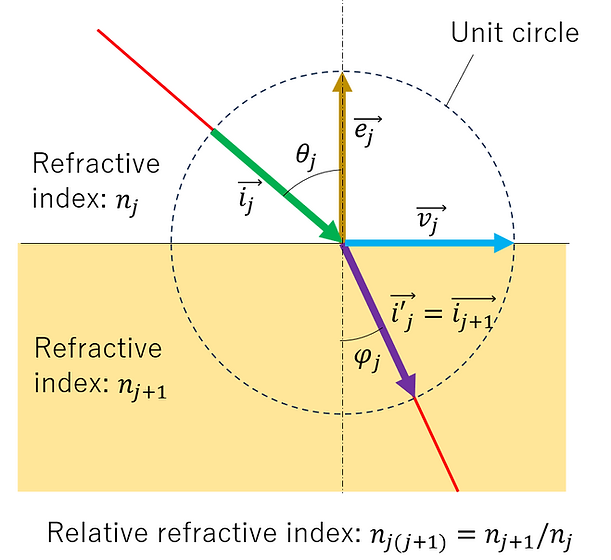
図に示されているように、第 j 番目の境界面の透過光は、その次の面への入射光となるので、⑥で得られた導出結果を用いて、以下の漸化式が得られるので、複数の透過面を透過した後の光線の方向ベクトルを最終的に求めることができる。

ここで、各ベクトルの成分を以下のように置く。

このとき、⑦は以下のように表すことができる。
