平行光を一点に集光するミラー形状
平行光を一点に集光するミラー形状は、回転放物面であることは広く知られている。ここでは、そのようになる幾何学的な原理について、別のコンテンツで示したベクトル理論を用いて導出していく。
平行光を一点 O に結像させるミラー面 S について考える。
平行光の方向ベクトルを以下のように定義する。

一点�に結像される点Oの座標を以下のように定義する。
ミラー面 S 上の任意の点を以下のように定義する。
このとき、ミラー面 S 上の任意の点における反射光の方向ベクトルは以下のように表される。

また、ミラー面 S の法線ベクトルは以下のように表される[1]。

ここまで示した条件を図示すると、以下のようになる。

ここで、上記の各ベクトル間には以下の関係がある。
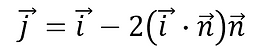
よって、

各成分について取り出すと以下のようになる。

①、②、③より、x≠0, y≠0, z≠0 のとき、
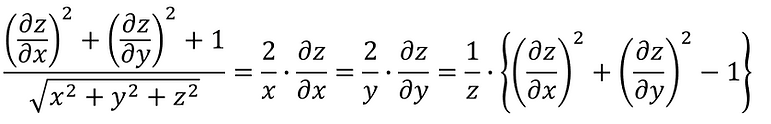
ゆえに、
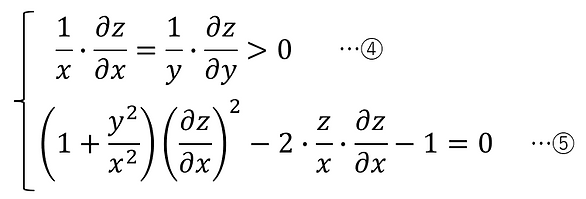
④より、

この偏微分方程式の解き方について以下に説明する[2]。
求める微分方程式を以下にように表されるとする。

このとき、以下の補助方程式を考える。

この補助方程式の解を以下のように表されるとする。

これを用いて、求める微分方程式の一般解を以下のように得ることができる。

ここで、φは任意の関数を意味する。
④においては以下のようになる。

よって、④における補助微分方程式は以下のようになる。

両辺を積分をして解くと、以下のようになる。

よって、④の一般解は以下のようになる。

ここで、以下のように置く。

このとき、z 中の変数は r のみとなるから、

⑤��へ代入して、

ここで、以下のように置く。

このとき、
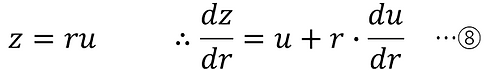
よって、

ここで、④、⑥、⑧より、

よって、

両辺を積分して、

ここで、任意の u に対して、

よって、絶対値記号を外すことができ、

⑦を式に戻すと、
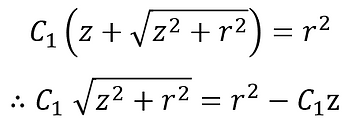
両辺を二乗して整理すると、

r>0( ∵ x≠0, y≠0) より、

ゆえに、

ここまでの導出は x≠0 and y≠0 and z≠0 の場合に対して行ったが、この導出結果を①、②、③に代入すると、x=0 and/or y=0 のときも成り立つ。
この形状は、回転放物面と言われている。
図示すると以下のようになる。
