top of page
ガウシアンビームが半径αのアパーチャを通るときの、中心軸からの距離 r に対する強度分布を以下のように表す。

ここで、wはビーム半径、i0=i(0)である。wは強度がi0(0)/(e^2)となるときのrの値で定義される。
半径 α のアパーチャを遠った後の光量 V(α)は、バウムクーヘン積分法[1]により以下のように計算できる。

また、アパーチャを遠る前の光量 V0 は、上式においてα→∞とした結果に等しく、以下のようになる。

よって、アパーチャを通る前後の光量比は次のように表される。

特に、α=wのときの値は次のようになる。

このように、ビーム径でアパーチャを決めた場合は、約13.5%の光量をロスすることになる。
一方、α=2wのときは次のようになり、アパーチャによる蹴られは殆ど無視できる量となる。
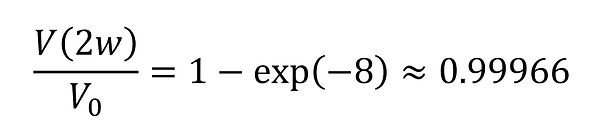
このため、ガウシアンビームを光学素子に通す際は、ビーム径の2倍を網羅する有効域を確保することが求められる。
-
参考文献
bottom of page
