top of page

Relations for plane-parallel plates derived from Snell's law

Various equations can be derived from the law of refraction of light at material interfaces (Snell's law). Here we introduce some practical ones.

  • Image position of convergent light incident perpendicularly on a plane-parallel plate

The position of the real image relative to the virtual image is determined for two cases: when the real image is inside the plane-parallel plate, and when it is beyond the plane-parallel plate.

A ray diagram of light rays passing through a plane-parallel plate is shown along with a virtual image.

(1) When the real image is in a plane-parallel plate:

平行平面板と結像位置の関係_042.png

*For dimensional notation, see Appendix: Direction and sign of one-dimensional vectors and angles

Here, dh, dθ1, and dθ2 are assumed to be minute quantities.

The conditions shown in the figure can be expressed as the following equations:

平行平面板と結像位置の関係_043.png

Here, the second equation is Snell's law. Also, since dθ1 and dθ2 are infinitesimal quantities, the following can be said:

Description of light rays entering a material_003.png

So the original equation can be replaced with:

平行平面板と結像位置の関係_044.png

Solving this leads to the following:

Relationship between parallel plane plate and image position_013.png

(2) When the real image is beyond the plane-parallel plate:

平行平面板と結像位置の関係_045.png

*For dimensional notation, see Appendix: Direction and sign of one-dimensional vectors and angles

Here, dh, dθ1, and dθ2 are assumed to be minute quantities.

The conditions shown in the figure can be expressed as the following equations:

平行平面板と結像位置の関係_046.png

Here, the second equation is Snell's law. Also, since dθ1 and dθ2 are infinitesimal quantities, the following can be said:

Description of light rays entering a material_003.png

So the original equation can be replaced with:

平行平面板と結像位置の関係_047.png

Solving this leads to the following:

The difference between the position of a light ray passing through a plane-parallel plate and the position of a virtual image

  • Image position when a parallel plate is placed at an angle to the optical axis

Consider the following light beam that is obliquely incident on a parallel plane plate and forms an image at the exit point. Calculate Δx and Δy in this case.

平行平面板斜め入射_015.png

Here, dh, dθ1 , and dθ2 are small quantities.

The conditions shown in the figure can be expressed as follows:

平行平面板斜め入射_016.png

Here, we will explain the formula for ④. Because dθ1 and dθ2 are minute, if we consider the red line and the green dotted line to be parallel, the width of the light beam before it enters the boundary surface will be cosθ1 /cosθ2 times the width of the light beam after it passes through the boundary surface, as shown below. Taking this into consideration, we have formulated ④.

平行平面板斜め入射_021.png

Differentiate both sides of ③ to get

From ①, ②, ③', ④, and ⑤, eliminating s, xA, xB, x0, dh, dθ1, and dθ2, we get

平行平面板斜め入射_017.png

Here, from ① and ⑥,

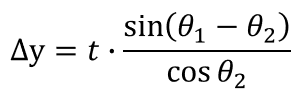
Also, from ③,

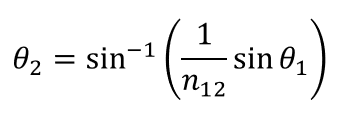
Therefore, the solution we seek can be expressed as follows:

平行平面板斜め入射_018.png

Furthermore, by applying ③ and eliminating θ2, we get

平行平面板斜め入射_019.png
Lateral shift of a ray of light passing through a plane-parallel plate

As a specific example, if θ1 =45[deg] and n=1.5, the result will be as follows.

平行平面板斜め入射_020.png

  • Image position when a parallel plate is placed at an angle to the optical axis

Consider the following optical arrangement:

This shows the spherical aberration that occurs in a plane-parallel plate.

dθ1 and dθ2 are assumed to be minute amounts, and the longitudinal spherical aberration δs and the horizontal spherical aberration δx are calculated.

The conditions shown in the figure can be expressed as the following equations:

Relationship between parallel plane plate and image position_029.png

① and ③ represent Snell's law, and ⑤ represents the numerical aperture.

From ①, ②, and ⑤,

Relationship between parallel plane plate and image position_030.png

From ③ and ④,

Relationship between parallel plane plate and image position_031.png

From ②' and ④', the longitudinal spherical aberration is as follows:

Amount of longitudinal spherical aberration generated by a plane-parallel plate

From ⑥ and ⑦, the lateral spherical aberration is as follows:

Transverse spherical aberration generated by a plane-parallel plate

The amount of spherical aberration is shown in the diagram below: As can be seen from the diagram, for the same plate thickness, the amount of spherical aberration peaks when the relative refractive index is around 1.6.

Refractive index dependence of longitudinal spherical aberration generated by a plane-parallel plate
Refractive index dependence of transverse spherical aberration generated by a plane-parallel plate

Here, the influence of aberration will be considered.

The point image resolution (Airy disk radius) due to wave optics diffraction broadening is expressed by the following formula:

Amount of blurring of spots due to wave optics diffraction broadening

As a rough guideline, when δx is much smaller than δd , δd dominates the resolution, so the effect of δx is small. On the other hand, when δx is much larger than δd , δx dominates the resolution.

A graph comparing δx and δd is shown below. While this is only a rough guideline, at a wavelength of 532 nm, the effects of spherical aberration become dominant over the point image resolution due to diffraction spread when using cover glass (approximately 0.15 mm thick) with an NA of 0.32 or higher, and when using glass with a thickness of 1.5 mm with an NA of 0.18 or higher. At a wavelength of 1064 nm, the effects of spherical aberration become dominant over the point image resolution due to diffraction spread when using cover glass (approximately 0.15 mm thick) with an NA of 0.38 or higher, and when using glass with a thickness of 1.5 mm with an NA of 0.22 or higher.

Comparison of spot blur due to lateral spherical aberration and diffraction spread when NA is a variable
bottom of page