Ray propagation in spherical lens systems based on paraxial calculations
A ray in the paraxial region has a very small angle θ with respect to the optical axis of the optical system, and all of its paths pass very close to the optical axis. In this case, the following approximation holds for θ:
sin θ = θ, tan θ = θ, cos θ = 1
Therefore, limiting the area to the paraxial region makes ray tracing calculations extremely simple and is useful for understanding the structure of the optical system. Here, we will show how to derive the calculation formula.
・Derivation of the paraxial calculation formula
When a ray of light passes through the boundary surface (spherical shape) of a material, the ray of light in the paraxial region can be illustrated as follows:
(i) When u > 0, u' > 0,

Figure 1-1
(ii) When u > 0, u' < 0,

Figure 1-2
*For dimensional notation, refer to Appendix: Definition of direction and sign of one-dimensional vectors and angles
The parameters in the above figure are defined as follows:
n : Refractive index of the material before incidence on the boundary surface
n' : Refractive index of the material after exiting the boundary surface
r : Radius of curvature of the boundary surface
u: The angle between the incident ray on the boundary surface and the central axis (counterclockwise is positive)
u': Angle between the exit ray from the boundary surface and the central axis (counterclockwise is positive)
i: The angle between the incident light on the boundary surface and the normal to the boundary surface (counterclockwise is positive)
i': The angle between the light emitted from the boundary surface and the normal to the boundary surface (counterclockwise is positive)
φ: The angle between the normal at the incident position of the ray on the boundary surface and the central axis (counterclockwise is positive)
h: Height of the ray at the boundary surface relative to the central axis
s: The distance from the boundary surface to the point where the incident light intersects with the central axis
s': Distance from the boundary surface to the point where the light emitted from the boundary surface intersects with the central axis
Here, the angles u , u' , φ , i , i' and the height h are assumed to be sufficiently small. Also, the color coding for each parameter is as follows: the amount given by the setting is in blue, and the amount given by the calculation formula is in black (in the recurrence formula model shown later).
In this case, the conditions shown in the figure can be expressed as the following equations in both (i) and (ii).

Here, the fact that both (i) and (ii) are expressed by the same equation means that they are both forms of the same model, and it can be said that it is sufficient to consider either one of them.
From (1)-①abc, the following is derived.

Furthermore, according to Snell's law , the following can be said in the paraxial region:
From (1)-①'ab and (1)-②, the Abbe's invariant shown below can be derived.

This formula can be transformed as follows:

Applying (1)-①a to this, the following relationship is obtained.

・Derivation of Lagrange invariant
First, let's look at (1)-③ (Abbe's invariant). This equation describes a ray of light going from point P to point P', but we can see that it does not include u, u', or h. From this, we can say that in the paraxial region, any ray of light passing through point P goes to point P' (i.e., points P and P' are in a conjugate relationship). This is shown again in the diagram below.
Furthermore, when the original entire system is rotated about point O (the spherical center of the boundary surface), and point P moves to point Q, and point P' moves to point Q', points Q and Q' are also in a conjugate relationship. However, since the boundary surface does not change at all before and after rotating the entire system, it can be said that points Q and Q' before rotating the entire system are also in a conjugate relationship.
Here, in the paraxial region, the arcs PQ and P'Q' can be regarded as straight lines perpendicular to the central axis, and therefore the PQ vector and P'Q' vector are vectors perpendicular to the central axis.

Figure 2-1
For each parameter, those shown in Figures 1-1 and 1-2 will be followed, and new parameters will be defined as follows.
y: object height
y': image height
ω: Angle of the ray from the object height y toward the intersection of the boundary surface and the optical axis
ω': Angle of the ray from the intersection of the boundary surface and the optical axis toward image height y'
In this case, the conditions shown in the figure can be expressed as the following equations:

Furthermore, according to Snell's law, the following can be said in the paraxial region:
From (1)-①a, (2)-①ab, and (2)-②, the following relationship can be obtained.

This relation is called the Lagrange invariant or the Helmholtz-Lagrange invariant.
・Recurrence formula for paraxial calculation
Consider a system in which a ray passes through the 0th surface (object surface), the 1st surface, the 2nd surface, ..., the j-th surface, ..., and the k-th surface (image surface) in that order. Here, each surface is assumed to be spherical (flat surfaces are given with an infinite radius of curvature). In this case, if we illustrate the ray in the paraxial region before and after passing through the j-th surface, it looks like this:
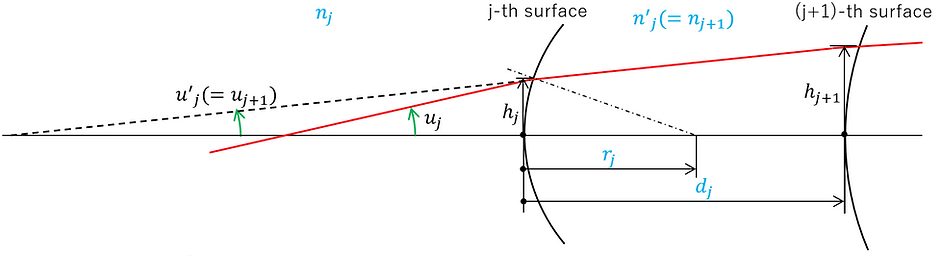
The parameters in the above figure are defined as follows:
*For dimensional notation, refer to Appendix: Definition of direction and sign of one-dimensional vectors and angles
The subscript j of each parameter means the j-th boundary surface.
For each parameter in the above figure, those shown in Figure 1-1 and Figure 1-2 will be followed, and new ones will be defined as follows.
dj : Distance from the j-th surface to the (j+1)-th surface
Here, the angles uj , u'j , and the height hj are assumed to be sufficiently small. For each parameter, the amount given by the setting is in blue, and the amount given by the calculation formula is in black.
First, from (1)-③'', the following can be said about the j-th plane:
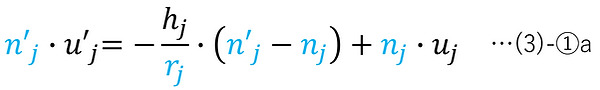
Furthermore, the following can be said from the figure.

Here, we put it as follows:

Applying this to (3)-①ab, we obtain the following equation.

(3)-① a'b' can be expressed as a matrix as follows.

By integrating (3)-①'ab, we obtain the following recurrence formula.

Next, from (2)-③ (Lagrange invariant), the following is true on the j-th surface:

Here, since n'j=nj+1 , u'j=uj+1 , and y'j=yj+1, the following can also be said:

From (3)-③④, the following can be said:

・Deriving optical system parameters through paraxial calculations
Here, the initial conditions and output values are given for the following two cases.
(i) In the case of parallel light incidence
In this case, as shown in the figure below, the initial condition of the recurrence formula (exiting the object surface) and the terminal condition of the recurrence formula (exiting the k-th surface) are given, and the focal length f is obtained as the output value of the optical system parameter.

From (1)-①a,

Therefore, dk can be calculated as follows:

Also, from the figure, the focal length f can be calculated as follows:

Here, in the case of parallel light incidence, d0 does not affect subsequent calculations. Also, in the definition of the paraxial region, h0 is an infinitesimal quantity, but the calculation of the focal length does not depend on the value of h0 (not just on infinitesimal quantities) .
(ii) In the case of a finite system
In this case, as shown in the figure below, the initial condition of the recurrence formula (exiting the object surface) and the terminal condition of the recurrence formula (exiting the k-th surface) are given, and the magnification β is obtained as the output value of the optical system parameter.

From (1)-①a,

Therefore, dk can be calculated as follows:

From (3)-⑤ (Lagrange invariant), the magnification β can be calculated as follows:
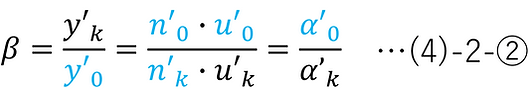
Here, in the definition of the paraxial region, u'0 is an infinitesimal quantity, but the calculation of the magnification does not depend on the value of u'0 (not just on infinitesimal quantities).
The calculation format based on what has been explained so far is shown below.
・Example: Formula for calculating the focal length of a single lens
Here, we will derive the formula for calculating the focal length of a single lens from the paraxial calculation formula. If we apply the refractive index of the material, n, the radius of curvature of the first and second surfaces, r1 and r2, respectively, and the center thickness, d1, to the paraxial calculation model, we get the figure below.
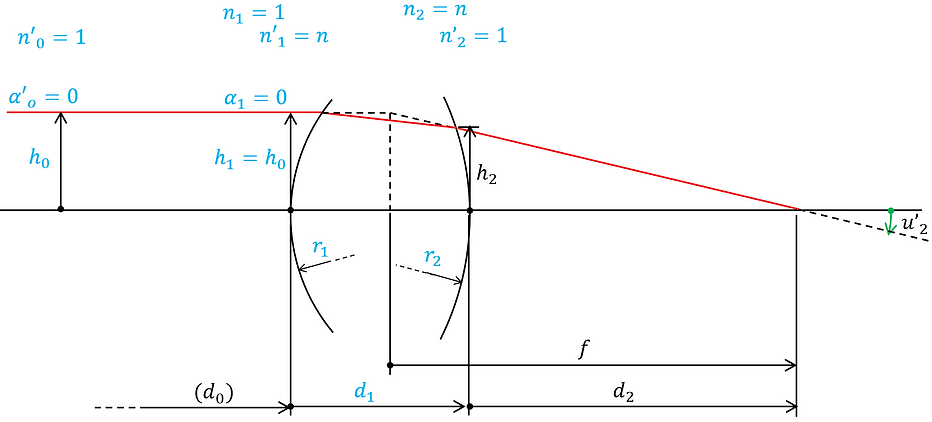
First, the following paraxial calculation formula is obtained from (3)-①'ab and (3)-①''.

Furthermore, from (4)-1-①②, the following is obtained:

Applying the parameter values in the figure (h1=h0 , n1=n'2=1, n'1 =n2=n, α1=0) to (5)-① gives the following:

From (5)-②ab, (5)-③, and n'2 =1 in the figure, the following is obtained.

The obtained (5)-②b' is called the Lens-Maker's Formula.