top of page

Mirror shape that focuses parallel light to a single point

It is widely known that the mirror shape that focuses parallel light to a single point is a paraboloid of revolution. Here, we will derive the geometric principle that makes it so using vector theory, which was shown in another content.

Consider a mirror surface S that focuses parallel light onto a point O.
The direction vector of parallel light is defined as follows.

Mirror shape that focuses parallel light to a single point_001.png

The coordinates of point O that is imaged to a single point are defined as follows:

Mirror shape that focuses parallel light to a single point_002.png

Any point on the mirror surface S is defined as follows:

Mirror shape that focuses parallel light to a single point_003.png

In this case, the direction vector of the reflected light at any point on the mirror surface S is expressed as follows:

Mirror shape that focuses parallel light to a single point_004.png

Moreover, the normal vector of the mirror surface S is expressed as follows [1]:

Mirror shape that focuses parallel light to a single point_005.png

The conditions described above can be illustrated as follows:

This shows the vectors set up to derive the principles for a mirror shape that focuses parallel light to a single point, i.e., a paraboloid of revolution.

Here, the following relationships exist between the above vectors:

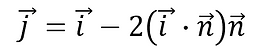
Mirror shape that focuses parallel light to a single point_006.png

Therefore,

When each component is extracted, it looks like this:

Mirror shape that focuses parallel light to a single point_008.png

From ①, ②, and ③, when x≠0, y≠0, z≠0,

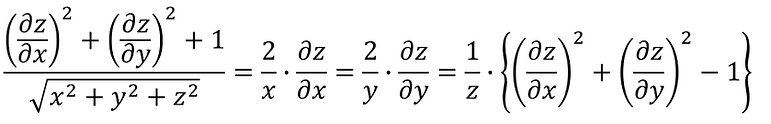
Mirror shape that focuses parallel light to a single point_009.png

Therefore,

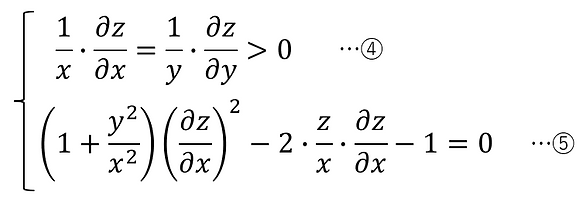
Mirror shape that focuses parallel light to a single point_010.png

From ④,

Mirror shape that focuses parallel light to a single point_011.png

The method for solving this partial differential equation will be explained below [2].

The desired differential equation is expressed as follows:

Mirror shape that focuses parallel light to a single point_012.png

In this case, consider the following auxiliary equation:

Mirror shape that focuses parallel light to a single point_013.png

Let the solution of this auxiliary equation be expressed as follows:

Mirror shape that focuses parallel light to a single point_014.png

Using this, we can obtain the general solution of the desired differential equation as follows:

Mirror shape that focuses parallel light to a single point_015.png

Here, φ denotes an arbitrary function.

In ④, it becomes as follows:

Mirror shape that focuses parallel light to a single point_016.png

Therefore, the auxiliary differential equation in ④ becomes:

Mirror shape that focuses parallel light to a single point_017.png

Integrating both sides and solving, we get the following:

Mirror shape that focuses parallel light to a single point_018.png

Therefore, the general solution to ④ is as follows.

Mirror shape that focuses parallel light to a single point_019.png

Here, we put it as follows:

Mirror shape that focuses parallel light to a single point_020.png

In this case, the only variable in z is r, so

Mirror shape that focuses parallel light to a single point_021.png

Substituting into ⑤,

Mirror shape that focuses parallel light to a single point_022.png

Here, we put it as follows:

Mirror shape that focuses parallel light to a single point_023.png

At this time,

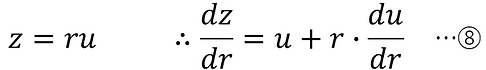
Mirror shape that focuses parallel light to a single point_024.png

Therefore,

Here, from ④, ⑥, and ⑧,

Mirror shape that focuses parallel light to a single point_026.png

Therefore,

Mirror shape that focuses parallel light to a single point_027.png

Integrating both sides,

Mirror shape that focuses parallel light to a single point_028.png

Now, for any u,

Mirror shape that focuses parallel light to a single point_029.png

Therefore, we can remove the absolute value sign,

Mirror shape that focuses parallel light to a single point_030.png

Putting ⑦ back into the equation,

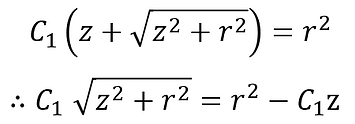
Mirror shape that focuses parallel light to a single point_031.png

Square both sides and rearrange,

Mirror shape that focuses parallel light to a single point_032.png

Since r＞0 (∵ x≠0, y≠0),

Therefore,

The derivation up to this point has been performed for the case where x≠0 and y≠0 and z≠0, but if we substitute the results of this derivation into ①, ②, and ③, it also holds when x=0 and/or y=0.

This shape is called a paraboloid of revolution, or a circular paraboloid.

This is illustrated below.

This shows the vectors set up to derive the principles for a mirror shape that focuses parallel light to a single point, i.e., a paraboloid of revolution.
bottom of page