Light loss when passing a Gaussian beam through a circular aperture
Consider the light loss when a Gaussian beam passes through a circular aperture, as shown in the figure below.

When a Gaussian beam passes through an aperture of radius α, the intensity distribution with respect to the distance r from the central axis is expressed as follows:

Here, w is the beam radius, i0 = i(0), and w is defined as the value of r when the intensity is i0(0)/ (e^2).
The amount of light V(α) after leaving an aperture of radius α can be calculated using the "shell integration method"[1] as follows:

In addition, the amount of light V0 before it leaves the aperture is equal to the result of changing α →∞ in the above equation, and is given by:

Therefore, the ratio of the amount of light before and after passing through the aperture is expressed as follows:

In particular, when α = w, the value is:

In this way, when the aperture is determined based on the beam waist radius, approximately 13.5 % of the light amount is lost.
On the other hand, when α = 2w, the following occurs, and the amount of shading due to the aperture becomes almost negligible.
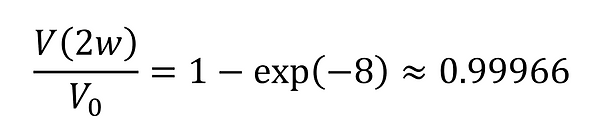
For this reason, when a Gaussian beam is passed through an optical element, it is necessary to ensure an effective area that covers twice the beam waist radius.
-
References