光波のコヒーレンス長の導出
ここでは、光波のコヒーレンス長(可干渉距離)と光源スペクトル幅の関係を、以下の2つのケースについて導出していきます。
<1>光源スペクトルが正規分布の場合
<2>スペクトル幅の広い光源の帯域をバンドパスフィルタで制限する場合(即ちステップ形状のスペクトル)
ここで、OCT(Optical Coherence Tomography)における深さ分解能は<1>のモデルから導出された値が一般的に採用されていますので、<1>の後半でこちらについても示します。OCTでは測定物から反射してくる光を検出するため往復のパスとなり、深さ分解能はコヒーレンス長の半分の値となる点には要注意です。
<1>光源スペクトルが正規分布の場合
ステップ1:k空間におけるスペクトル幅の導出
光波のスペクトル特性を、以下のようにk空間(波数空間)における正規分布(ガウス分布)として表す。

ここで、I0 は光波の全強度、kp は S(k) がピークとなる波数、wは k空間におけるスペクトルの標準偏差である。
S(k)を図示すると以下のようになる。

ここで、以下のように定義する。
・kH±はS(k)がピークの半分となるときの波数
・ΔkはS(k)の半値全幅
このとき、

よって、
ステップ2:λ空間におけるスペクトル幅の導出
①において、k=2π / λ, kp = 2π / λp として、 λ空間(波長空間)に変換すると、次のようになる。
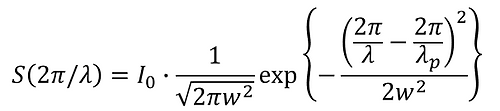
S(2π/λ)を図示すると以下のようになる。

ここで、以下のように定義する。
・λH±はS(2π/λ)がピークの半分となるときの波長
・ΔλはS(2π/λ)の半値全幅
このとき、
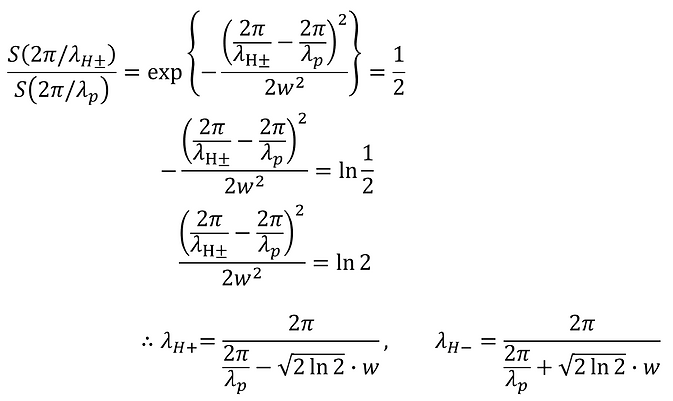
よって、

ステップ3:実空間におけるコヒーレンス長の導出
実空間(x空間)における光波の分布をE(x)とする。
また、振幅がピークとなる位置をxp、位置xpにおける位相を -δ とする。
このとき、

ここで、以下のことは自明である(奇関数の性質より)。

ゆえに、

ここで、以下のようにおく。

積分と微分の順序交換の定理[1]より、以下のことが言える。

この式を解くと以下のようになる。


ここで、

よって、

ゆえに、

E(x) を図示すると以下のようになる。

ここで、以下のように定義する。
・EA±(x)はE(x)の振幅
・xH±はEA±(x) がピークの半分となるときの位置
・ΔxはEA±(x)の半値全幅
このとき、

よって、

ステップ4�:ΔxとΔλの関係の導出
②と③より、最終的に以下の関係式が得られる。

※右辺の係数0.88の値はΔxとΔλの定義の仕方で若干変わります。
ΔxとΔλの関係を図示すると、以下のようになる。

応用:OCTの深さ分解能とコヒーレンス長の関係
OCT(Optical Coherence Tomography)における深さ分解能は光源スペクトルが正規分布のモデルで得られた④式から導出された値が一般的に採用されているので、ここでOCTの深さ分解能とコヒーレンス長の関係について示す。以下の図に示すように、屈折率nの物質中の観察面からの反射光を観察するとき、深さ分解能Δdとコヒーレンス長Δxの関係について考える。

ここまで求めてきたコヒーレンス長Δxは空気中における距離なので、物質中の距離に対しては空気換算長で考える必要がある。また、反射光を観察する場合は往復の距離になるので、光路長は実際の距離の2倍となる。このことを加味すると、コヒーレンス長と深さ分解能の関係は以下のようになる。

これを④に代入して、以下の式が得られる[2][3]。

<2>スペクトル幅の広い光源の帯域をバンドパスフィルタで制限する場合(即ちステップ形状のスペクトル)
ステップ1:k空間におけるスペクトル幅の導出
光波のスペクトル特性を、以下のようにk空間(波数空間)におけるステップ形状の分布として表す。
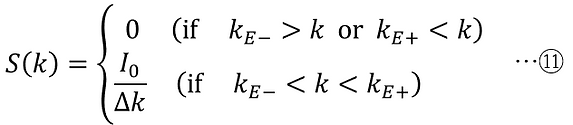
但し、

ここで、I0 は光波の全強度、kp は k空間におけるスペクトル帯域の中間の波数、kE±はそれぞれスペクトル帯域の端の波数、Δkはスペクトル帯域の幅である。
S(k)を図示すると以下のようになる。

ステップ2:λ空間におけるスペクトル幅の導出
⑪において、k=2π / λ, kE± = 2π / λE̠∓ とし、 λ空間(波長空間)に変換すると、次のようになる。
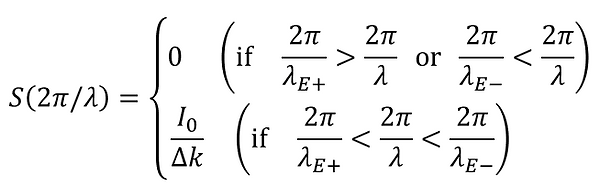
但し、

更に、以下のようにおく。

このとき、ΔλとΔkの関係は以下のように導出される。

よって、S(2π/λ)は以下のようになる。

S(2π/λ)を図示すると以下のようになる。

ステップ3:実空間におけるコヒーレンス長の導出
実空間(x空間)における光波の分布をE(x)とする。
また、振幅がピークとなる位置をxp、位置xpにおける位相を -δ とする。
このとき、

E(x) を図示すると以下のようにな��る。

ここで、EA±(x)はE(x)の振幅である。
この場合のコヒーレンス長の定義方法については、以下の2通りが考えられる。
(i) メインローブ全幅の半分をコヒーレンス長 ΔxA と定義する場合
xp に対し ± 2π / Δk でEA+(x)はゼロになる(このゼロ点間の幅をメインローブ全幅とする)。その半分の ± π / Δk では、EA+(x)はピークに対し 2/π 倍となるが、このときの幅 2π / Δk をコヒーレンス長 ΔxA と定義する。
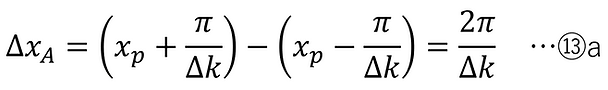
(ii) メインローブの半値全幅をコヒーレンス長 ΔxB と定義する場合
ΔxBは以下のように計算できる。

これは解析的に解くことは難しいので、数値的に求めると、以下のようになる。

ステップ4:ΔxとΔλの関係の導出
(i) コヒーレンス長を ΔxA で定義した場合
⑫、⑬aより、

(ii) コヒーレンス長を ΔxB で定義した場合
⑫、⑬bより、
